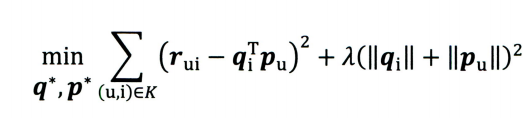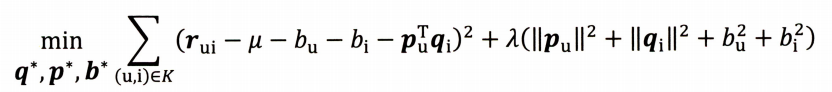MF(矩阵分解)算法概述
在之前我们介绍了协调过滤算法,但由于协调过滤存在以下问题:
协调过滤处理稀疏矩阵的能力较弱
协调过滤中,相似度矩阵维护难度大(物品和用户数量都比较大)
协调过滤算法的头部效应强
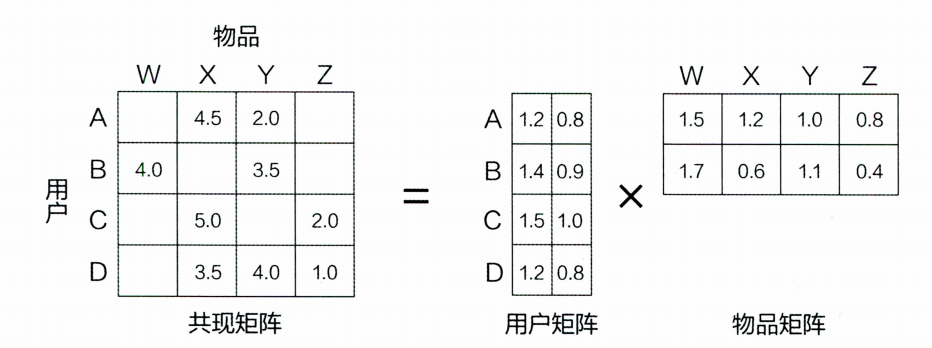
为了解决这些问题,我们提出了矩阵分解算法。其解决问题的大致思路是:希望为每个用户和物品生成一个隐向量,将用户和物品定位到隐向量的表示空间上,距离相近的用户和物品表面兴趣特点接近,应该把距离相近的视频推荐给目标用户。下面举例说明:3 ∗ 5 ( 令 k = 5 ) 3*5(令k=5) 3 ∗ 5 ( 令 k = 5 ) 5 ( k ) ∗ 3 5(k)*3 5 ( k ) ∗ 3
这里的隐向量是不可解释的,并不是如上图所示可以给用户和物品打上具体的标签,这是需要模型自己去学习的。
隐向量个数k决定了隐向量的表达能力的强弱,k越大,表达的信息就越强,用户的兴趣和物品的分类划分的越具体。
r ^ u i = q i T p u {\hat{r}}_{ui}=q_{i}^{T}p_{u}
r ^ u i = q i T p u
其中p u p_{u} p u q i q_{i} q i
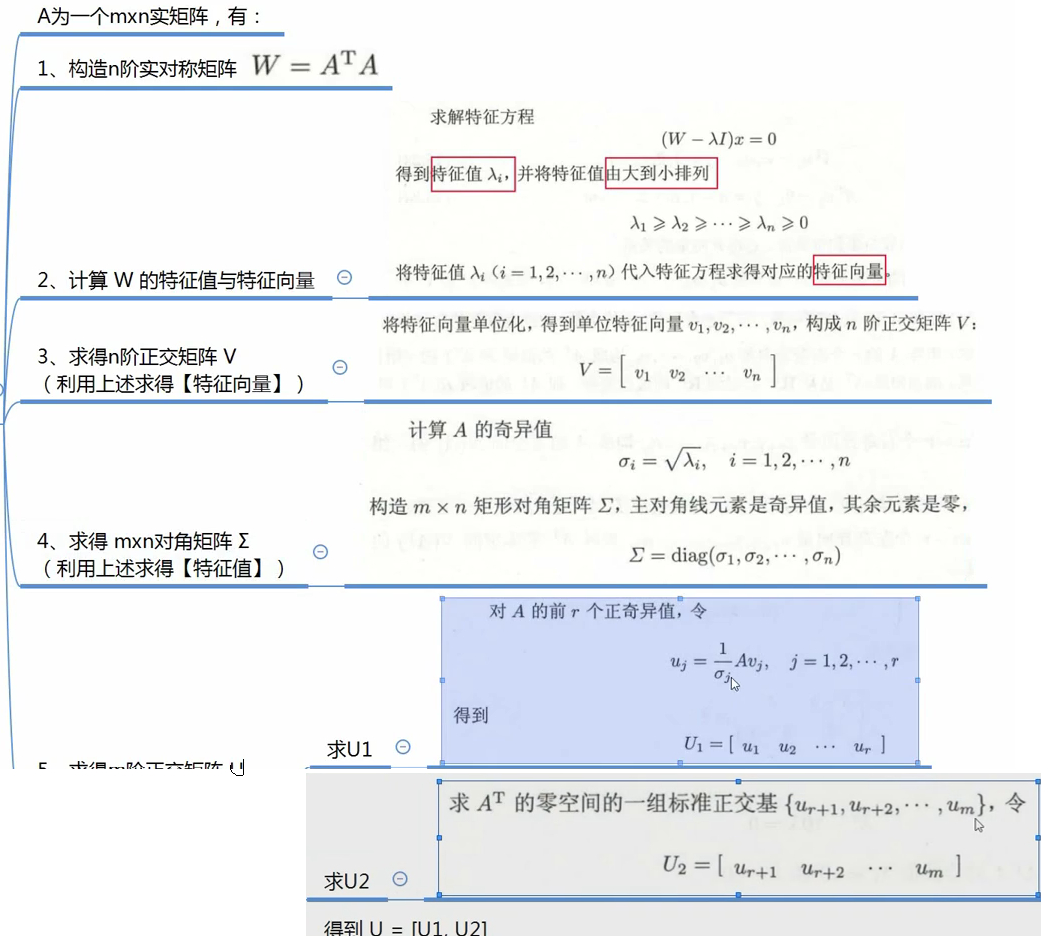
矩阵分解的求解
特征值分解
首先我们引入特征值,特征向量的概念
A v = λ v Av=\lambda v
A v = λ v
其中A是方阵,v是A的特征向量,λ \lambda λ
A = Q Σ Q − 1 A=Q\Sigma Q^{-1}
A = Q Σ Q − 1
其中Q是该矩阵的特征向量组成的矩阵,Σ \Sigma Σ
SVD 奇异值分解
O ( m n 2 ) O(mn^{2}) O ( m n 2 )
BaseSVD
基于我们上文的评分函数构造出损失函数:
LFM
由于不同用户的打分体系不同,有的人认为打3分已经是很低的分数了,二而有的人认为打1分才是比较差的评价,再加上不同物品的衡量标准也有所区别,比如电子产品和日用品的评分标准就回会很大,为了消除用户和物品打分的偏差,我们在君子分解时加入用户和物品的偏差向量,则我们的预测评分变成了:
r u i = u + b i + b u + q i T p u r_{ui}=u+b_{i}+b_{u}+q_{i}^{T}p_{u}
r u i = u + b i + b u + q i T p u
其中u是全局偏差常数,可使用评分的全局平均分,b i b_{i} b i b u b_{u} b u
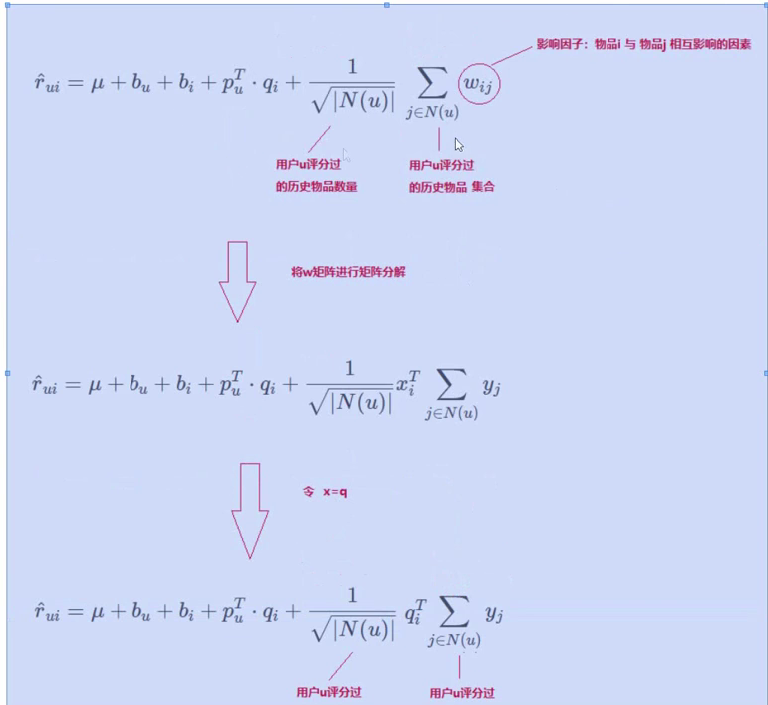
SVD++
由于物品之间可能存在某种关联性,这种关联性可能会影响物品的评分,(比如之前看过一部电影,就可能对他的续作也产生不错的印象,从而给打较高的分),所以SVD++就引入了用户评过分的历史物品,将这些物品间的相似度也考虑了进去。
1.问题引入
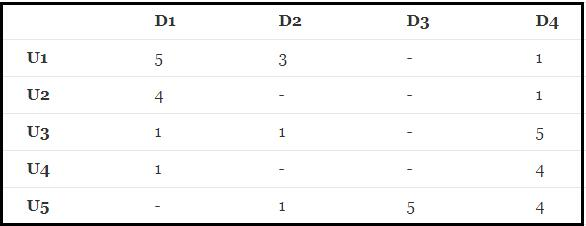
有如下R(5,4)矩阵:("-"表示用户没有打分)
2.问题分析
2.1构造损失函数
为了求出未打分的值,可以将矩阵R(n,m)分解为P(n,k)*Q(K,m),所以可以得到一个预测值R ^ = P ∗ Q \hat{R}=P*Q R ^ = P ∗ Q R ^ \hat{R} R ^ R ^ − R \hat{R}-R R ^ − R R ^ ≈ R \hat{R}\approx{R} R ^ ≈ R
L o s s ( P , Q ) = 1 2 ( R − R ^ ) 2 = 1 2 ( ∑ i = 1 m ∑ j = 1 n ( R i j − ∑ s = 1 k P i s Q j s ) ) 2 Loss(P,Q)=\frac{1}{2}(\hat{R-R})^2=\frac{1}{2}(\sum_{i=1}^{m}\sum_{j=1}^{n}({R_{ij}-\sum_{s=1}^{k}P_{is}Q_{js}}))^{2}
L oss ( P , Q ) = 2 1 ( R − R ^ ) 2 = 2 1 ( i = 1 ∑ m j = 1 ∑ n ( R ij − s = 1 ∑ k P i s Q j s ) ) 2
2.1梯度下降
梯度下降法的核心思想即是沿函数的导数方向的不断改变自身参数,从到最终能到达最低点。梯度下降法的一些注意事项在多元线性回归 中做了一些介绍,有兴趣可以查看。
∂ ∂ P i k L ( P , Q ) \frac{\partial}{\partial{P_{ik}}}L(P,Q) ∂ P ik ∂ L ( P , Q ) = 1 2 ( R i j − ∑ k = 1 k P i k Q k j ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ ∑ k = 1 k P i k Q k j ) ∂ P i k ) =\frac{1}{2}(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})*2*(-1)*(\frac{\partial{\sum_{k=1}^{k}P_{ik}Q_{kj}})}{\partial{P_{ik}}}) = 2 1 ( R ij − ∑ k = 1 k P ik Q kj ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ P ik ∂ ∑ k = 1 k P ik Q kj ) ) = − ( R i j − ∑ k = 1 k P i k Q k j ) Q k j =-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj} = − ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ∂ ∂ Q k j L ( P , Q ) \frac{\partial}{\partial{Q_{kj}}}L(P,Q) ∂ Q kj ∂ L ( P , Q ) = 1 2 ( R i j − ∑ k = 1 k P i k Q k j ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ ∑ k = 1 k P i k Q k j ) ∂ P k j ) =\frac{1}{2}(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})*2*(-1)*(\frac{\partial{\sum_{k=1}^{k}P_{ik}Q_{kj}})}{\partial{P_{kj}}}) = 2 1 ( R ij − ∑ k = 1 k P ik Q kj ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ P kj ∂ ∑ k = 1 k P ik Q kj ) ) = − ( R i j − ∑ k = 1 k P i k Q k j ) P i k =-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik} = − ( R ij − ∑ k = 1 k P ik Q kj ) P ik
应用梯度下降法不断修改当前参数值:P i k = P i k − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) P_{ik}=P_{ik}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj}) P ik = P ik − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ) = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj}) = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) Q kj )
Q k j = P i k − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) Q_{kj}=P_{ik}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik}) Q kj = P ik − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) P ik ) = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik}) = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) P ik ) α \alpha α
2.3正则化
当训练的数据不够时或特征数量大于样本数量时,就会出现过拟合的情况,我们为了解决过拟合,就会采用正则化的手段或者减少一些非必要的样本特征。常用的有L1范数和L2范数。∣ ∣ x ∣ ∣ p = ( ∑ i n ∣ x i ∣ p ) 1 p ||x||_{p}=(\sum_{i}^{n}|x_{i}|^{p})^{\frac{1}{p}} ∣∣ x ∣ ∣ p = ( ∑ i n ∣ x i ∣ p ) p 1 ∣ ∣ x 1 ∣ ∣ = ∑ i = 1 n ∣ x i ∣ ||x_{1}||=\sum_{i=1}^{n}|x_{i}| ∣∣ x 1 ∣∣ = ∑ i = 1 n ∣ x i ∣ ∣ ∣ x 2 ∣ ∣ = ( ∑ i = 1 n ∣ x i ∣ 2 ) 1 2 ||x_{2}||=(\sum_{i=1}^{n}|x_{i}|^{2})^{\frac{1}{2}} ∣∣ x 2 ∣∣ = ( ∑ i = 1 n ∣ x i ∣ 2 ) 2 1
J ( θ ) = 1 2 m [ ∑ i = 1 m ( y i − h θ ( x i ) ) 2 + λ ∑ j = 1 n ∣ θ j ∣ ] J({\theta})=\frac{1}{2m}[\sum_{i=1}^{m}{(y^{i}-h_{\theta}(x^{i}))^{2}+\lambda\sum_{j=1}{n}|\theta_{j}|}]
J ( θ ) = 2 m 1 [ i = 1 ∑ m ( y i − h θ ( x i ) ) 2 + λ j = 1 ∑ n ∣ θ j ∣ ]
L2正则化:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( y i − h θ ( x i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J({\theta})=\frac{1}{2m}[\sum_{i=1}^{m}{(y^{i}-h_{\theta}(x^{i}))^{2}+\lambda\sum_{j=1}{n}\theta_{j}^{2}}]
J ( θ ) = 2 m 1 [ i = 1 ∑ m ( y i − h θ ( x i ) ) 2 + λ j = 1 ∑ n θ j 2 ]
式子中m为样本数量,n为特征个数。
3.代码实现
1 2 import numpy as npimport matplotlib.pyplot as plt
1 2 3 4 5 6 7 8 9 10 11 12 13 R=np.array([[5 ,3 ,0 ,1 ], [4 ,0 ,0 ,1 ], [1 ,1 ,0 ,5 ], [1 ,0 ,0 ,4 ], [0 ,1 ,5 ,4 ]]) M=R.shape[0 ] N=R.shape[1 ] K=2 P=np.random.rand(M,K) Q=np.random.rand(K,N) print (P)print (Q)
[[0.65360868 0.08726216]
[0.69762591 0.03076026]
[0.88861613 0.75595254]
[0.31559948 0.49104854]
[0.33077934 0.40914307]]
[[0.68124148 0.49563369 0.14058849 0.73546283]
[0.31494592 0.86798718 0.48578754 0.95628464]]
L o s s = 1 2 ( R − P Q ) 2 = 1 2 ( ∑ i = 1 m ∑ j = 1 n ( R i j − ∑ s = 1 k P i s Q j s ) ) 2 Loss=\frac{1}{2}(R-PQ)^{2}=\frac{1}{2}(\sum_{i=1}^{m}\sum_{j=1}^{n}({R_{ij}-\sum_{s=1}^{k}P_{is}Q_{js}}))^{2}
L oss = 2 1 ( R − PQ ) 2 = 2 1 ( i = 1 ∑ m j = 1 ∑ n ( R ij − s = 1 ∑ k P i s Q j s ) ) 2
1 2 3 4 5 6 7 8 9 def cost (R,P,Q ): e=0 for i in range (R.shape[0 ]): for j in range (R.shape[1 ]): if (R[i,j]>0 ): e+=(R[i,j]-np.dot(P[i,:],Q[:,j]))**2 return e/2
L2正则化:
L o s s = 1 2 ( R − P Q ) 2 = 1 2 ( ∑ i = 1 m ∑ j = 1 n ) R i j − ∑ s = 1 k P i s Q j s ) 2 + λ 2 ∑ s = 1 k ( P i k 2 + Q k j 2 ) Loss=\frac{1}{2}(R-PQ)^{2}=\frac{1}{2}(\sum_{i=1}^{m}\sum_{j=1}^{n}){R_{ij}-\sum_{s=1}^{k}P_{is}Q_{js}})^{2}+\frac{\lambda}{2}\sum_{s=1}{k}({P_{ik}^{2}}+Q_{kj}^{2})
L oss = 2 1 ( R − PQ ) 2 = 2 1 ( i = 1 ∑ m j = 1 ∑ n ) R ij − s = 1 ∑ k P i s Q j s ) 2 + 2 λ s = 1 ∑ k ( P ik 2 + Q kj 2 )
1 2 3 4 5 6 7 8 9 10 def cost_re (R,P,Q,lambda1 ): e=0 for i in range (R.shape[0 ]): for j in range (R.shape[1 ]): if (R[i][j]>0 ): e+=(R[i,j]-np.dot(P[i,:],Q[:,j]))**2 for k in range (P.shape[1 ]): e+=lambda1*(P[i,k]**2 +Q[k,j]**2 )/2 return e/2
对损失函数求偏导:∂ ∂ P i k L ( P , Q ) \frac{\partial}{\partial{P_{ik}}}L(P,Q) ∂ P ik ∂ L ( P , Q ) = 1 2 ( R i j − ∑ k = 1 k P i k Q k j ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ ∑ k = 1 k P i k Q k j ) ∂ P i k ) =\frac{1}{2}(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})*2*(-1)*(\frac{\partial{\sum_{k=1}^{k}P_{ik}Q_{kj}})}{\partial{P_{ik}}}) = 2 1 ( R ij − ∑ k = 1 k P ik Q kj ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ P ik ∂ ∑ k = 1 k P ik Q kj ) ) = − ( R i j − ∑ k = 1 k P i k Q k j ) Q k j =-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj} = − ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ∂ ∂ Q k j L ( P , Q ) \frac{\partial}{\partial{Q_{kj}}}L(P,Q) ∂ Q kj ∂ L ( P , Q ) = 1 2 ( R i j − ∑ k = 1 k P i k Q k j ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ ∑ k = 1 k P i k Q k j ) ∂ P k j ) =\frac{1}{2}(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})*2*(-1)*(\frac{\partial{\sum_{k=1}^{k}P_{ik}Q_{kj}})}{\partial{P_{kj}}}) = 2 1 ( R ij − ∑ k = 1 k P ik Q kj ) ∗ 2 ∗ ( − 1 ) ∗ ( ∂ P kj ∂ ∑ k = 1 k P ik Q kj ) ) = − ( R i j − ∑ k = 1 k P i k Q k j ) P i k =-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik} = − ( R ij − ∑ k = 1 k P ik Q kj ) P ik P i k = P i k − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) P_{ik}=P_{ik}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj}) P ik = P ik − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ) = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj}) = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) Q kj )
Q k j = P i k − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) Q_{kj}=P_{ik}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik}) Q kj = P ik − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) P ik ) = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik}) = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) P ik )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def grad (R,P,Q,lr,epochs ): costList=[] for s in range (epochs+1 ): for i in range (R.shape[0 ]): for j in range (R.shape[1 ]): if (R[i][j]>0 ): e=R[i,j]-np.dot(P[i,:],Q[:,j]) for k in range (P.shape[1 ]): grad_p=e*Q[k][j] grad_q=e*P[i][k] P[i][k]=P[i][k]+lr*grad_p Q[k][j]=Q[k][j]+lr*grad_q if s%50 ==0 : e=cost(R,P,Q) costList.append(e) return P,Q,costList lr=0.0001 epochs=10000 p,q,costList=grad(R,P,Q,lr,epochs) print (np.dot(p,q))
[[5.06116901 2.87426131 2.43375669 1.00254423]
[3.96425112 2.26334177 2.08974137 0.96504113]
[1.0366021 0.90360134 5.30277467 4.91333664]
[0.99043153 0.81279639 4.2952649 3.93863408]
[1.64541544 1.19616657 4.78417292 4.23883696]]
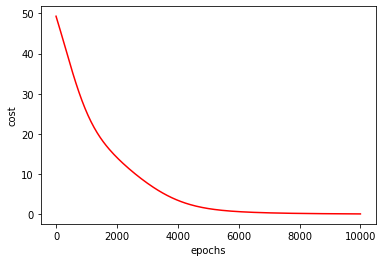
1 2 3 4 5 x=np.linspace(0 ,10000 ,201 ) plt.plot(x,costList,'r' ) plt.xlabel('epochs' ) plt.ylabel('cost' ) plt.show()
加入正则项后:P i k = P i k − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) + λ P i k P_{ik}=P_{ik}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik})+\lambda{P_{ik}} P ik = P ik − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) P ik ) + λ P ik = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) P i k ) − λ P i k =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})P_{ik})-\lambda{P_{ik}} = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) P ik ) − λ P ik Q k j = Q k j − α ∗ ( − ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) + λ Q k j Q_{kj}=Q_{kj}-\alpha*(-(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj})+\lambda{Q_{kj}} Q kj = Q kj − α ∗ ( − ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ) + λ Q kj = P i k + α ( R i j − ∑ k = 1 k P i k Q k j ) Q k j ) − λ Q k j =P_{ik}+\alpha(R_{ij}-\sum_{k=1}^{k}P_{ik}Q_{kj})Q_{kj})-\lambda{Q_{kj}} = P ik + α ( R ij − ∑ k = 1 k P ik Q kj ) Q kj ) − λ Q kj
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def grad_re (R,P,Q,lr,epochs,lambda1 ): costList=[] for s in range (epochs+1 ): for i in range (R.shape[0 ]): for j in range (R.shape[1 ]): if (R[i][j]>0 ): e=R[i,j]-np.dot(P[i,:],Q[:,j]) for k in range (P.shape[1 ]): grad_p=e*Q[k][j] grad_q=e*P[i][k] P[i][k]=P[i][k]+lr*grad_p-lambda1*P[i][k] Q[k][j]=Q[k][j]+lr*grad_q-lambda1*Q[k][j] if s%50 ==0 : e=cost_re(R,P,Q,lambda1) costList.append(e) return P,Q,costList lambda1=0.0001 p,q,costList=grad_re(R,P,Q,0.003 ,epochs,lambda1) print (np.dot(p,q))
[[4.92262848 2.9460198 2.02962105 1.00548811]
[3.9420148 2.37520018 1.85600337 0.99804788]
[1.00407789 0.99148638 6.03037773 4.90035828]
[0.99660486 0.90775439 4.8875762 3.94603309]
[1.15092516 1.00009806 4.95103649 3.97741499]]
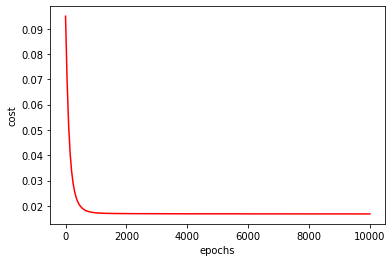
1 2 3 4 5 x=np.linspace(0 ,10000 ,201 ) plt.plot(x,costList,'r' ) plt.xlabel('epochs' ) plt.ylabel('cost' ) plt.show()
通过观察代价函数随迭代步数的变化图可以看出:进行正则化后的代价函数的图像比没有进行正则化的图像较为圆滑了些许,可以得出正则化确实是一种解决过拟合问题的一种手段。