1.一元线性回归
1.1.问题引入
根据不同房屋尺寸,预测出房子可以卖多少钱。所做任务就是通过给的数据集构建一个模型。
显然这是一个回归问题,根据之前的数据预测出一个准确的输出值。h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_{0}+\theta_{1}x h θ ( x ) = θ 0 + θ 1 x
1.2.代价函数
在线性回归中,最常用的是==均方误差==,其具体形式为:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( ( ^ y ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}{(\hat(y^{(i)})-y^{(i)})^{2}}=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{^{(i)}})-y^{(i)})^{2}} J ( θ 0 , θ 1 ) = 2 m 1 ∑ i = 1 m ( ( ^ y ( i ) ) − y ( i ) ) 2 = 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
我们的目标便是选出可以是代价函数J最小的模型参数。θ 0 = 0 \theta_{0}=0 θ 0 = 0 J ( θ 1 ) J(\theta_{1}) J ( θ 1 ) θ 1 \theta_{1} θ 1
1.3.梯度下降法
梯度下降法是一个用来求函数最小值的算法,其思想是:开始我们随机选取一个参数组合( θ 0 , θ 1 ) (\theta_{0},\theta_{1}) ( θ 0 , θ 1 )
其计算公式为:θ j = θ j − α ∗ ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j}=\theta_{j}-\alpha*\frac{\partial}{\partial\theta_{j}}J(\theta_{0},\theta_{1}) θ j = θ j − α ∗ ∂ θ j ∂ J ( θ 0 , θ 1 ) α \alpha α α \alpha α ∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial }{\partial \theta_j}J(\theta_0,\theta_1)=\frac{\partial}{\partial \theta_j}\frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})^2} ∂ θ j ∂ J ( θ 0 , θ 1 ) = ∂ θ j ∂ 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
θ 0 : j = 0 \theta_0:j=0 θ 0 : j = 0 ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})} ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) )
θ 1 : j = 1 \theta_1:j=1 θ 1 : j = 1 ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i ) \frac{\partial }{\partial \theta_1}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})*x^{(i)}} ∂ θ 1 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i )
应用梯度下降法修改不断当前值
θ 0 \theta_0 θ 0 θ 0 − α ∗ \theta_0-\alpha* θ 0 − α ∗ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})} ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) )
θ 1 \theta_1 θ 1 θ 1 − α ∗ \theta_1-\alpha* θ 1 − α ∗ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i ) \frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})*x^{(i)}} ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i ) θ 0 , θ 1 \theta_{0},\theta_{1} θ 0 , θ 1
实际使用中停止梯度下降方式:
①达到最大迭代次数后即停止梯度下降。
②当损失函数小于很小的预设值时,此时即可认为已经到达了最低点。
1.4实现
1.手工梯度下降法
1 2 3 import numpy as npimport matplotlib.pyplot as plt%matplotlib inline
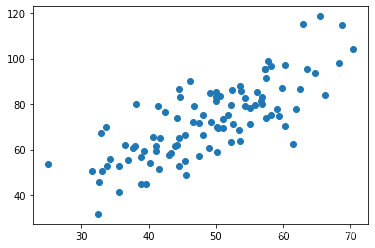
1 2 3 4 5 6 7 data=np.genfromtxt("/root/jupyter_projects/data/fangjia1.csv" ,delimiter=',' ) x_data=data[:,0 ] y_data=data[:,1 ] plt.scatter(x_data,y_data) plt.show()
1 2 3 4 5 6 7 8 9 lr=0.0001 theta_0=0 theta_1=0 epochs=50
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( ( ^ y ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}{(\hat(y^{(i)})-y^{(i)})^{2}}=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{^{(i)}})-y^{(i)})^{2}} J ( θ 0 , θ 1 ) = 2 m 1 ∑ i = 1 m ( ( ^ y ( i ) ) − y ( i ) ) 2 = 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
1 2 3 4 5 6 7 8 def compute_error (theta_0,theta_1,x_data,y_data ): totalError=0 for i in range (0 ,len (x_data)): totalError+=(theta_1*x_data[i]+theta_0-y_data[i])**2 totalError return totalError/float (2 *len (x_data))
对代价函数求偏导:∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial }{\partial \theta_j}J(\theta_0,\theta_1)=\frac{\partial}{\partial \theta_j}\frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})^2} ∂ θ j ∂ J ( θ 0 , θ 1 ) = ∂ θ j ∂ 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
θ 0 : j = 0 \theta_0:j=0 θ 0 : j = 0 ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})} ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) )
θ 1 : j = 1 \theta_1:j=1 θ 1 : j = 1 ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i ) \frac{\partial }{\partial \theta_1}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})*x^{(i)}} ∂ θ 1 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i )
应用梯度下降法修改不断当前值
θ 0 \theta_0 θ 0 θ 0 − α ∗ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \theta_0-\alpha*\frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})} θ 0 − α ∗ ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) )
θ 1 \theta_1 θ 1 θ 1 − α ∗ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i ) \theta_1-\alpha*\frac{\partial }{\partial \theta_0}J(\theta_0,\theta_1)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)})*x^{(i)}} θ 1 − α ∗ ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i )
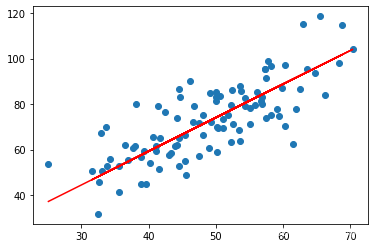
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def gradient_descent_runner (x_data,y_data,theta_0,theta_1,lr,epochs ): m=len (x_data) for i in range (epochs): theta_0_grad=0 theta_1_grad=0 for j in range (0 ,len (x_data)): theta_0_grad+=(1 /m)*((theta_1*x_data[j]+theta_0)-y_data[j]) theta_1_grad+=(1 /m)*((theta_1*x_data[j]+theta_0)-y_data[j])*x_data[j] theta_0=theta_0-(theta_0_grad*lr) theta_1=theta_1-(theta_1_grad*lr) if i%5 ==0 : print ("epochs:" ,i) plt.scatter(x_data,y_data) plt.plot(x_data,theta_1*x_data+theta_0,'r' ) plt.show() return theta_0,theta_1
1 2 3 4 5 6 7 8 9 10 11 print ("starting theta_0={0},theta_1={1},error={2}" .format (theta_0,theta_1,compute_error(theta_0,theta_1,x_data,y_data)))print ('running' )theta_0,theta_1=gradient_descent_runner(x_data,y_data,theta_0,theta_1,lr,epochs) print ("end{0} theta_0={1},theta_1={2},error={3}" .format (epochs,theta_0,theta_1,compute_error(theta_0,theta_1,x_data,y_data)))
starting theta_0=0,theta_1=0,error=2782.5539172416056
running
epochs: 0
epochs: 10
epochs: 20
epochs: 30
epochs: 40
epochs: 45
end50 theta_0=0.030569950649287983,theta_1=1.4788903781318357,error=56.32488184238028
2.sklearn实现
1 2 3 4 import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression%matplotlib inline
1 2 3 4 5 6 7 8 9 data=np.genfromtxt("/root/jupyter_projects/data/fangjia1.csv" ,delimiter=',' ) x_data=data[:,0 ] y_data=data[:,1 ] plt.scatter(x_data,y_data) plt.show() print (x_data.shape)
(100,)
1 2 3 4 x_data=data[:,0 ,np.newaxis] print (x_data.shape)y_data=data[:,1 ,np.newaxis]
(100, 1)
1 2 3 4 model=LinearRegression() theta=model.fit(x_data,y_data)
1 2 3 4 5 6 7 plt.scatter(x_data,y_data) plt.plot(x_data,model.predict(x_data),'r' ) plt.show() print (theta)print (model.coef_)print (model.intercept_)
2.多元线性回归
1.多元线性回归
对房价模型增加更多的特征,如房间数,楼层数等,构成了一个含有多变量的模型,模型中特征为( x 1 , x 2 . . . x n ) (x_{1},x_{2}...x_{n}) ( x 1 , x 2 ... x n )
其中n代表特征数量,m代表训练集中的实列数量。
x ( i ) x^{(i)} x ( i )
x j ( i ) x^{(i)}_{j} x j ( i )
多变量的回归的假设h为:h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n} h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ... + θ n x n x 0 = 1 x_{0}=1 x 0 = 1
$$X=\left[\begin{matrix}x_{0}\x_{1}\x_{2}\…\x_{n}\end{matrix}\right]$$ $$\theta=\left[\begin{matrix}\theta_{0}\\theta_{1}\\theta_{2}\…\\theta_{n}\end{matrix}\right]$$
则h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . θ n x n h_{\theta}(x)=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...\theta_{n}x_{n} h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ... θ n x n θ T X \theta^{T}X θ T X
接下来就要 求解θ \theta θ
1.梯度下降法
构造代价函数J ( θ 0 , θ 1 , . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\theta_{1},...\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2} J ( θ 0 , θ 1 , ... θ n ) = 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
运用梯度下降法:
θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , . . . , θ n ) \theta_{j}=\theta_{j}-\alpha \frac{\partial}{\partial\theta_{j}}J(\theta_{0},\theta_{1},...,\theta_{n}) θ j = θ j − α ∂ θ j ∂ J ( θ 0 , θ 1 , ... , θ n )
θ j = θ j − α ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \theta_{j}=\theta_{j}-\alpha \frac{\partial}{\partial\theta_{j}}\frac{1}{2m}\sum_{i=1}^{m}({h_{\theta}(x^{(i)})-y^{(i)}})^{2} θ j = θ j − α ∂ θ j ∂ 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2
θ j = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}=\theta_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}({h_{\theta}(x^{(i)})-y^{(i)}})x^{(i)}_{j} θ j = θ j − α m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )
2.正规方程
正规方程通过是通过对代价函数进行求导,并使其导数为0,来解得θ \theta θ θ = ( X T X ) − 1 X T y \theta=(X^{T}X)^{-1}X^{T}y θ = ( X T X ) − 1 X T y
当特征变量数目小于1万以下时,通常使用正规方程来求解,大于一万则使用梯度下降法。
2.梯度下降法实践
1.特征缩放
以房价为例,假设我们使用两个特征(房屋的尺寸大小和房间的数量),并且令θ 0 = 0 \theta_{0}=0 θ 0 = 0 0 — 2000 0—2000 0—2000 0 − 5 0-5 0 − 5
为了解决这个问题:就需要对特征进行缩放,如图:
x i = x − u i S i x_{i}=\frac{x-u_{i}}{S_{i}} x i = S i x − u i
其中u i u_{i} u i x i x_{i} x i S i S_{i} S i
2.学习率(learning rate)
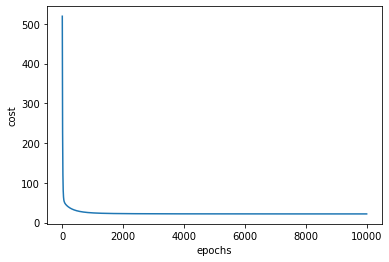
由于梯度下降法收敛所需的迭代次数无法提前预支。通常画出代价函数随迭代次数的图像来观察梯度下降法合适趋于收敛。
当然也可以自带测试收敛,即将代价函数的变化值与某个阈值$w$(如:0.001)来比较,如果小于该阈值则认为此时收敛。但是选择一个合适的阈值也是比较困,所有更多采用第一种方法。
当代价函数随迭代步数的图像如此变化时,说明此时$\alpha$偏大,应当选择一个稍微小一点的值。
当α \alpha α
尝试挑选的学习率:……,0.001,0.003,0.1,0.3,1,……
3.Boston房价预测
1 2 3 from sklearn import datasetsimport numpy as npimport matplotlib.pyplot as plt
1 2 3 4 5 6 7 8 9 10 11 12 13 boston=datasets.load_boston() x_data=boston.data y_data=boston.target print (x_data.shape)print (y_data.shape)for i in range (x_data.shape[1 ]): x_data[:,i]=(x_data[:,i]-x_data[:,i].mean())/(x_data[:,i].max ()-x_data[:,i].min ()) X=np.concatenate((np.ones((x_data.shape[0 ],1 )),x_data),axis=1 ) Y=y_data.reshape(-1 ,1 ) print (X.shape,Y.shape)print (X[:5 ,0 :])
(506, 13)
(506,)
(506, 14) (506, 1)
[[ 1. -0.0405441 0.06636364 -0.32356227 -0.06916996 -0.03435197
0.05563625 -0.03475696 0.02682186 -0.37171335 -0.21419304 -0.33569506
0.10143217 -0.21172912]
[ 1. -0.04030818 -0.11363636 -0.14907546 -0.06916996 -0.17632728
0.02612869 0.10633469 0.1065807 -0.32823509 -0.31724648 -0.06973762
0.10143217 -0.09693883]
[ 1. -0.0403084 -0.11363636 -0.14907546 -0.06916996 -0.17632728
0.17251688 -0.07698147 0.1065807 -0.32823509 -0.31724648 -0.06973762
0.09116942 -0.23794325]
[ 1. -0.0402513 -0.11363636 -0.32832766 -0.06916996 -0.19896103
0.13668626 -0.23455099 0.20616331 -0.28475683 -0.35541442 0.02600706
0.09570823 -0.26802051]
[ 1. -0.03983903 -0.11363636 -0.32832766 -0.06916996 -0.19896103
0.16523579 -0.14804224 0.20616331 -0.28475683 -0.35541442 0.02600706
0.10143217 -0.20207128]]
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)}-y^{(i)}))}^{2}
J ( θ ) = 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) − y ( i ) )) 2
∑ i = 1 2 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = ( y − x θ ) T ( y − x θ ) \sum_{i=1}^{2m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}=(y-x\theta)^{T}(y-x\theta)
i = 1 ∑ 2 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = ( y − x θ ) T ( y − x θ )
公式:$$(A+B)^{T}=A^{T}+B^{T}$$
( A B ) T = B T A T (AB)^{T}=B^{T}A^{T}
( A B ) T = B T A T
∂ J ( θ ) ∂ θ = ∂ ( y − x θ ) T ( y − x θ ) ∂ θ \frac{\partial J(\theta)}{\partial \theta}=\frac{\partial (y-x\theta)^{T}(y-x\theta)}{\partial \theta}
∂ θ ∂ J ( θ ) = ∂ θ ∂ ( y − x θ ) T ( y − x θ )
= ∂ ( y T y − y T x θ − θ T x T y + θ T x T x θ ) ∂ θ =\frac{\partial (y^{T}y-y^{T}x\theta-\theta^{T}x^{T}y+\theta^{T}x^{T}x\theta)}{\partial \theta} = ∂ θ ∂ ( y T y − y T x θ − θ T x T y + θ T x T x θ ) = ∂ y T y ∂ θ − ∂ y T x θ ∂ θ − ∂ θ T x T y ∂ θ + ∂ θ T x T x θ ∂ θ =\frac{\partial y^{T}y}{\partial \theta}-\frac{\partial y^{T}x\theta}{\partial \theta}-\frac{\partial \theta^{T}x^{T}y}{\partial \theta}+\frac{\partial \theta^{T}x^{T}x\theta}{\partial \theta} = ∂ θ ∂ y T y − ∂ θ ∂ y T x θ − ∂ θ ∂ θ T x T y + ∂ θ ∂ θ T x T x θ
分子布局:分子为列向量或者分母为行向量
分子布局
分母布局
∂ b T A x ∂ x \frac{\partial b^{T}Ax}{\partial x} ∂ x ∂ b T A x b T A b^{T}A b T A A T b A^{T}b A T b
∂ X T A X ∂ X \frac{\partial X^{T}AX}{\partial X} ∂ X ∂ X T A X X T ( A + A T ) X^{T}(A+A^{T}) X T ( A + A T ) ( A + A T ) X (A+A^{T})X ( A + A T ) X
∂ y T y ∂ θ = 0 \frac{\partial y^{T}y}{\partial \theta}=0 ∂ θ ∂ y T y = 0
∂ y T x θ ∂ θ = x T y \frac{\partial y^{T}x\theta}{\partial \theta}=x^{T}y ∂ θ ∂ y T x θ = x T y
应为θ T x T y \theta^{T}x^{T}y θ T x T y ∂ θ T x T y ∂ θ = ( ∂ θ T x T y ) T ∂ θ = ∂ y T x θ ∂ θ = x T y \frac{\partial \theta^{T}x^{T}y}{\partial \theta}=\frac{(\partial \theta^{T}x^{T}y)^{T}}{\partial \theta}=\frac{\partial y^{T}x\theta}{\partial \theta}=x^{T}y ∂ θ ∂ θ T x T y = ∂ θ ( ∂ θ T x T y ) T = ∂ θ ∂ y T x θ = x T y
∂ θ T x T x θ ∂ θ = ( x T x + ( x T x ) T ) θ = 2 x T x θ \frac{\partial \theta^{T}x^{T}x\theta}{\partial \theta}=(x^{T}x+(x^{T}x)^{T})\theta=2x^{T}x\theta ∂ θ ∂ θ T x T x θ = ( x T x + ( x T x ) T ) θ = 2 x T x θ
∂ J ( θ ) ∂ θ = X T X θ − X T y \frac{\partial J(\theta)}{\partial \theta}=X^{T}X\theta-X^{T}y
∂ θ ∂ J ( θ ) = X T Xθ − X T y
直接令J=0θ \theta θ
θ = ( X T X ) − 1 X T Y \theta=(X^{T}X)^{-1}X^{T}Y
θ = ( X T X ) − 1 X T Y
1 2 theta=np.random.rand(14 ,1 ) print (theta)
[[0.59826263]
[0.7714136 ]
[0.96782367]
[0.05007622]
[0.28160071]
[0.59145316]
[0.86688075]
[0.32402074]
[0.83781872]
[0.9972824 ]
[0.03729666]
[0.3470009 ]
[0.35738919]
[0.25179409]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 learning_rate=0.0001 epochs=10000 costList=[] for i in range (epochs): grad_theta=np.matmul(X.T,np.matmul(X,theta)-Y) theta=theta-learning_rate*grad_theta if (i%10 ==0 ): cost=np.mean(np.square(Y-np.matmul(X,theta))) costList.append(cost) ep=np.linspace(0 ,epochs,1000 ) print (costList[-1 ])plt.plot(ep,costList) plt.xlabel('epochs' ) plt.ylabel('cost' ) plt.show()
21.901811902045843
array([[ 22.53280632],
[ -8.60798018],
[ 4.47504867],
[ 0.50817969],
[ 2.71178142],
[ -8.41145881],
[ 20.00501683],
[ 0.09039972],
[-15.82506381],
[ 6.74485343],
[ -6.25266277],
[ -8.92882317],
[ 3.73796887],
[-19.13688284]])
1 2 3 4 5 6 Xmat=np.matrix(X) Ymat=np.matrix(Y) xt=Xmat.T*Xmat w=xt.I*X.T*Y w
matrix([[ 22.53280632],
[ -9.60975755],
[ 4.64204584],
[ 0.56083933],
[ 2.68673382],
[ -8.63457306],
[ 19.88368651],
[ 0.06721501],
[-16.22666104],
[ 7.03913802],
[ -6.46332721],
[ -8.95582398],
[ 3.69282735],
[-19.01724361]])
1 2 cost=np.mean(np.square(Ymat-Xmat*w)) cost
21.894831181729206






![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2JG7rjll-1641220068004)(output_7_9.png)]](https://img-blog.csdnimg.cn/08aadcf4a1c84e328e56c8d6ea835929.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5piv5b-Y55Sf5ZWK,size_12,color_FFFFFF,t_70,g_se,x_16)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S1bQzLt5-1641220068008)(output_7_17.png)]](https://img-blog.csdnimg.cn/2b1b6af72a574defad0b2a6a8d6511a5.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5piv5b-Y55Sf5ZWK,size_12,color_FFFFFF,t_70,g_se,x_16)