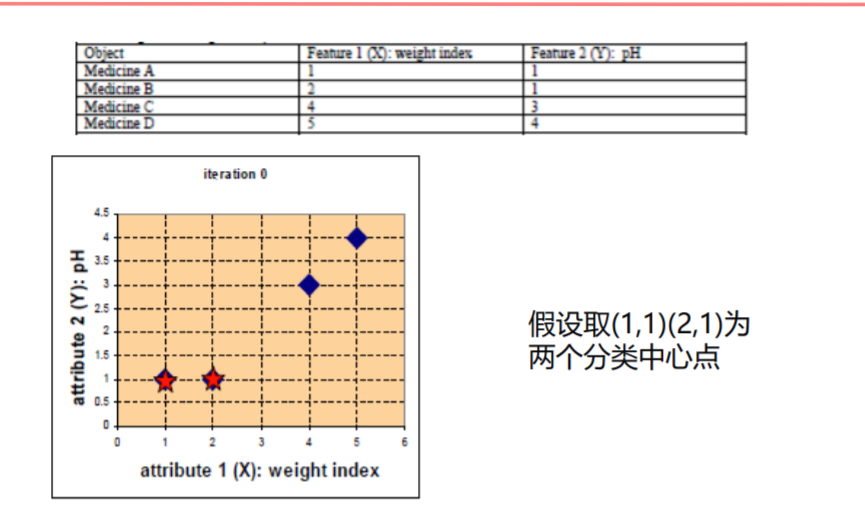
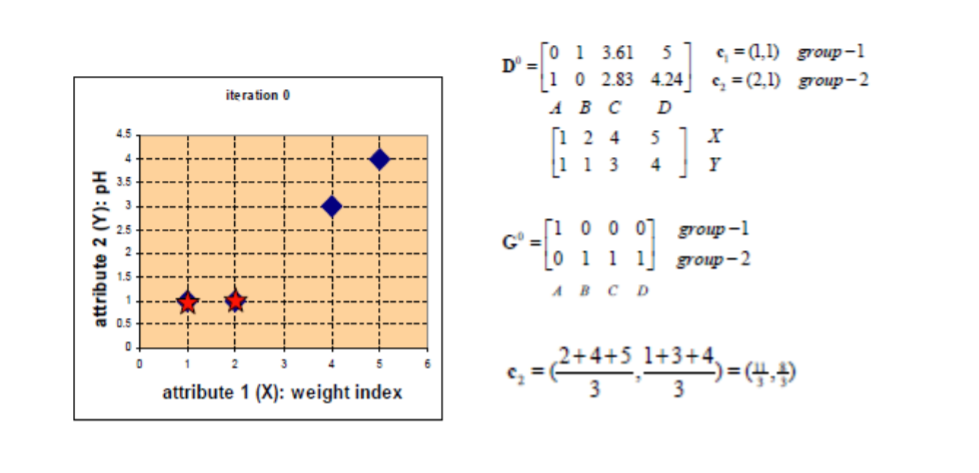
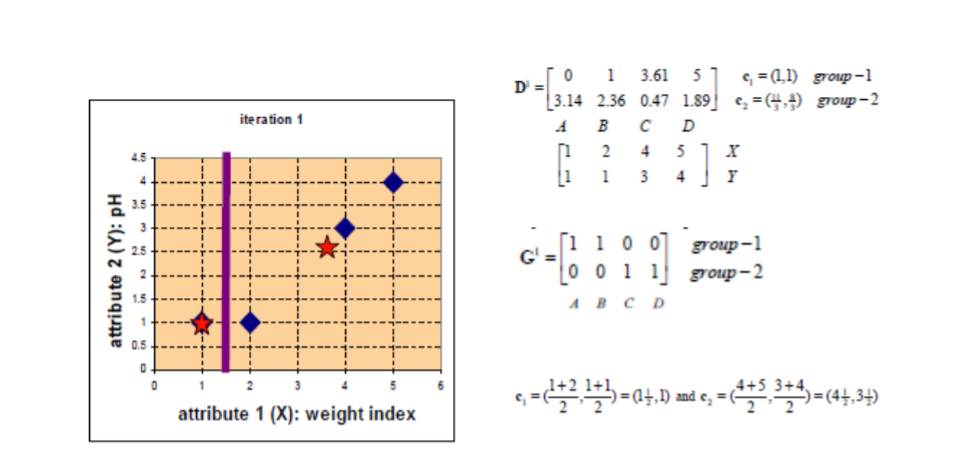
聚类是一种无监督学习。与分类不同的是,分类的数据集都是有标签的已经指明了该样本是哪一类,而对于聚类其数据集样本是没有标签的,需要我们根据特征对这些数据进行聚类。
1.K-Means算法
算法接受参数K,然后将事先输入的n个数据对象划分成K个聚类以便使得所获得得聚类满足:同一聚类中得对象相似的较高,而不同聚类中的对象相似度较小。
python实现
1 2 import numpy as npimport matplotlib.pylab as plt
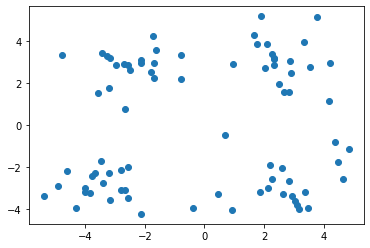
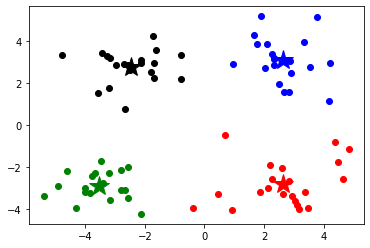
1 2 3 4 5 6 data=np.genfromtxt('kmeans.txt' ,delimiter=' ' ) print (data.shape)print (data[:5 ,:])plt.scatter(data[:,0 ],data[:,1 ]) plt.show()
(80, 2)
[[ 1.658985 4.285136]
[-3.453687 3.424321]
[ 4.838138 -1.151539]
[-5.379713 -3.362104]
[ 0.972564 2.924086]]
1 2 def eucldistance (v1,v2 ): return np.sqrt(sum ((v2-v1)**2 ))
1 2 3 4 5 6 7 8 9 10 11 12 13 def initCenter (data,k ): numSanples,dim=data.shape center=np.zeros((k,dim)) for i in range (k): index=int (np.random.uniform(0 ,numSanples)) center[i,:]=data[index,:] return center
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 def kmeans (data,k ): numSamples=data.shape[0 ] resultData=np.array(np.zeros((numSamples,2 ))) isChange=True center=initCenter(data,k) while (isChange): isChange=False for i in range (numSamples): Mindist=10000 minindex=0 for j in range (k): distance=eucldistance(center[j,:],data[i,:]) if (distance<Mindist): Mindist=distance resultData[i,1 ]=distance minindex=j if resultData[i,0 ] !=minindex: isChange=True resultData[i,0 ]=minindex for j in range (k): cluster_index=np.nonzero(resultData[:,0 ]==j) point=data[cluster_index] center[j,:]=np.mean(point,axis=0 ) return center,resultData
1 2 3 4 test=np.array([0 ,1 ,2 ,3 ,1 ,0 ,2 ,3 ,1 ,2 ,0 ,1 ]) print (test==0 )print (np.nonzero(test==0 ))print (test[np.nonzero(test==0 )])
[ True False False False False True False False False False True False]
(array([ 0, 5, 10], dtype=int64),)
[0 0 0]
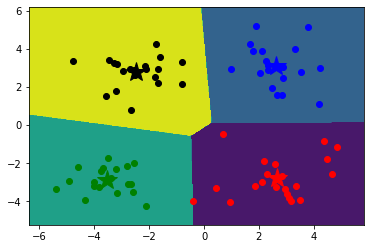
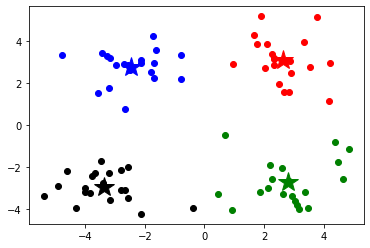
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def showCluster (data, k, centroids, resultData ): numSamples, dim = data.shape if dim != 2 : print ("dimension of your data is not 2!" ) return 1 mark = ['or' , 'ob' , 'og' , 'ok' , '^r' , '+r' , 'sr' , 'dr' , '<r' , 'pr' ] if k > len (mark): print ("Your k is too large!" ) return 1 for i in range (numSamples): markIndex = int (resultData[i, 0 ]) plt.plot(data[i, 0 ], data[i, 1 ], mark[markIndex]) mark = ['*r' , '*b' , '*g' , '*k' , '^b' , '+b' , 'sb' , 'db' , '<b' , 'pb' ] for i in range (k): plt.plot(centroids[i, 0 ], centroids[i, 1 ], mark[i], markersize = 20 ) plt.show()
1 2 3 4 k=4 center,resultData=kmeans(data,k) showCluster(data,k,center,resultData)
array([[-3.68133264, -3.18226857],
[ 2.39738441, 1.74393033],
[ 3.104819 , -3.107608 ],
[-2.5978898 , 1.81264996]])
1 2 3 def predict (datas ): return np.array([np.argmin(((np.tile(data,(k,1 ))-center)**2 ).sum (axis=1 )) for data in datas])
1 2 3 4 x_test=[1 ,2 ] a=np.tile(x_test,[k,1 ]) print (a)print ((a**2 ).sum (axis=1 ))
[[1 2]
[1 2]
[1 2]
[1 2]]
[5 5 5 5]
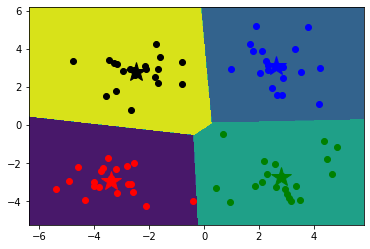
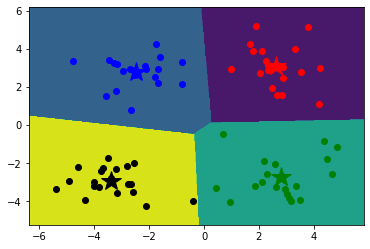
1 2 3 4 5 6 7 8 9 10 11 12 x_min, x_max = data[:, 0 ].min () - 1 , data[:, 0 ].max () + 1 y_min, y_max = data[:, 1 ].min () - 1 , data[:, 1 ].max () + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02 ), np.arange(y_min, y_max, 0.02 )) z = predict(np.c_[xx.ravel(), yy.ravel()]) z=z.reshape(xx.shape) cs=plt.contourf(xx,yy,z) showCluster(data,k,center,resultData)
sklearn实现
1 from sklearn.cluster import KMeans
1 2 data=np.genfromtxt('kmeans.txt' ,delimiter=' ' ) k=4
1 2 3 model=KMeans(n_clusters=k) model.fit(data)
KMeans(n_clusters=4)
1 2 3 centers=model.cluster_centers_ centers
array([[-3.38237045, -2.9473363 ],
[ 2.6265299 , 3.10868015],
[ 2.80293085, -2.7315146 ],
[-2.46154315, 2.78737555]])
1 2 3 result=model.predict(data) result
array([1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3,
2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0,
1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3,
2, 0, 1, 3, 2, 0, 1, 3, 2, 0, 1, 3, 2, 0])
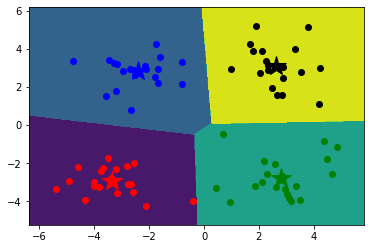
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 x_min, x_max = data[:, 0 ].min () - 1 , data[:, 0 ].max () + 1 y_min, y_max = data[:, 1 ].min () - 1 , data[:, 1 ].max () + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02 ), np.arange(y_min, y_max, 0.02 )) z = model.predict(np.c_[xx.ravel(), yy.ravel()]) z=z.reshape(xx.shape) cs=plt.contourf(xx,yy,z) mark = ['or' , 'ob' , 'og' , 'ok' , '^r' , '+r' , 'sr' , 'dr' , '<r' , 'pr' ] for i in range (data.shape[0 ]): plt.plot(data[i, 0 ], data[i, 1 ], mark[result[i]]) mark = ['*r' , '*b' , '*g' , '*k' , '^b' , '+b' , 'sb' , 'db' , '<b' , 'pb' ] for i in range (k): plt.plot(centers[i, 0 ], centers[i, 1 ], mark[i], markersize = 20 ) plt.show()
2.Mini Batch K-Means
Mini Batch K-Means 算法是K—Means算法的变种,采用小批量的数据子集减小计算时间。这里的小批量是指每次训练算法时所随机抽取的数据子集,采用这些随机产生的子集进行训练,大大减少了计算时间,结果一般只略差与标准算法。
sklearn实现
1 from sklearn.cluster import MiniBatchKMeans
1 2 3 data=np.genfromtxt('kmeans.txt' ,delimiter=' ' ) model1=MiniBatchKMeans(n_clusters=4 ) model1.fit(data)
MiniBatchKMeans(n_clusters=4)
1 2 centers1=model1.cluster_centers_ centers1
array([[-3.35355922, -2.94580235],
[-2.38894596, 2.82134059],
[ 2.79165315, -2.79705023],
[ 2.61970115, 3.11412341]])
1 2 result1=model1.predict(data) print (result1)
[3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3
1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1 2 0 3 1
2 0 3 1 2 0]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 x_min, x_max = data[:, 0 ].min () - 1 , data[:, 0 ].max () + 1 y_min, y_max = data[:, 1 ].min () - 1 , data[:, 1 ].max () + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02 ), np.arange(y_min, y_max, 0.02 )) z = model1.predict(np.c_[xx.ravel(), yy.ravel()]) z=z.reshape(xx.shape) cs=plt.contourf(xx,yy,z) mark = ['or' , 'ob' , 'og' , 'ok' , '^r' , '+r' , 'sr' , 'dr' , '<r' , 'pr' ] for i in range (data.shape[0 ]): plt.plot(data[i, 0 ], data[i, 1 ], mark[result1[i]]) mark = ['*r' , '*b' , '*g' , '*k' , '^b' , '+b' , 'sb' , 'db' , '<b' , 'pb' ] for i in range (k): plt.plot(centers1[i, 0 ], centers1[i, 1 ], mark[i], markersize = 20 ) plt.show()
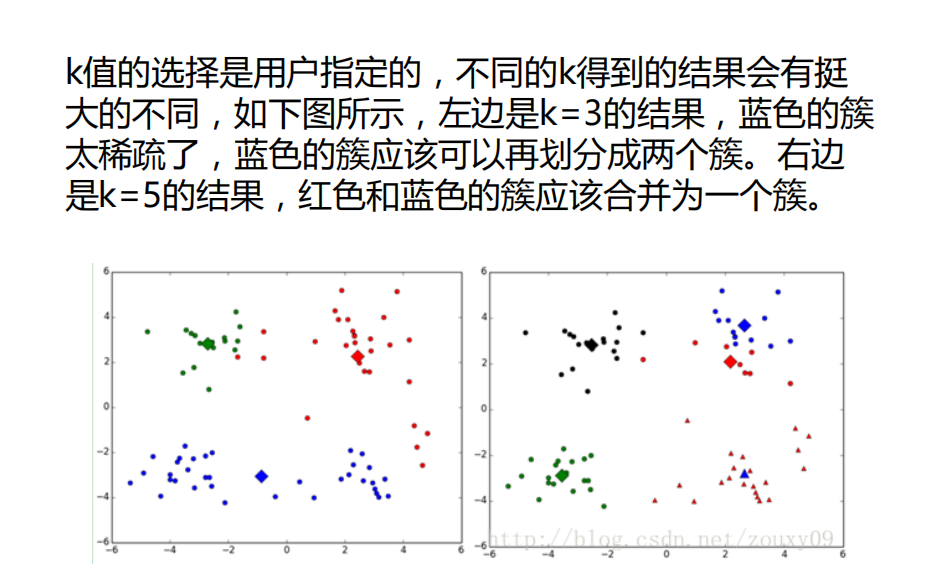
3.K-Means 算法问题
1.对于K个初始质心的选择比较敏感,容易陷入局部最小值
对于K个初始质心的选择比较敏感,容易陷入局部最小值。
1 2 import numpy as npimport matplotlib.pylab as plt
1 2 3 data=np.genfromtxt('kmeans.txt' ,delimiter=' ' ) print (data.shape)print (data[:5 ,:])
(80, 2)
[[ 1.658985 4.285136]
[-3.453687 3.424321]
[ 4.838138 -1.151539]
[-5.379713 -3.362104]
[ 0.972564 2.924086]]
1 2 def eucldistance (v1,v2 ): return np.sqrt(sum ((v2-v1)**2 ))
1 2 3 4 5 6 7 8 9 10 11 12 13 def initCenter (data,k ): numSanples,dim=data.shape center=np.zeros((k,dim)) for i in range (k): index=int (np.random.uniform(0 ,numSanples)) center[i,:]=data[index,:] return center
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 def kmeans (data,k ): numSamples=data.shape[0 ] resultData=np.array(np.zeros((numSamples,2 ))) isChange=True center=initCenter(data,k) while (isChange): isChange=False for i in range (numSamples): Mindist=10000 minindex=0 for j in range (k): distance=eucldistance(center[j,:],data[i,:]) if (distance<Mindist): Mindist=distance resultData[i,1 ]=distance minindex=j if resultData[i,0 ] !=minindex: isChange=True resultData[i,0 ]=minindex for j in range (k): cluster_index=np.nonzero(resultData[:,0 ]==j) point=data[cluster_index] center[j,:]=np.mean(point,axis=0 ) return center,resultData
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def showCluster (data, k, centroids, resultData ): numSamples, dim = data.shape if dim != 2 : print ("dimension of your data is not 2!" ) return 1 mark = ['or' , 'ob' , 'og' , 'ok' , '^r' , '+r' , 'sr' , 'dr' , '<r' , 'pr' ] if k > len (mark): print ("Your k is too large!" ) return 1 for i in range (numSamples): markIndex = int (resultData[i, 0 ]) plt.plot(data[i, 0 ], data[i, 1 ], mark[markIndex]) mark = ['*r' , '*b' , '*g' , '*k' , '^b' , '+b' , 'sb' , 'db' , '<b' , 'pb' ] for i in range (k): plt.plot(centroids[i, 0 ], centroids[i, 1 ], mark[i], markersize = 20 ) plt.show()
1 2 3 def predict (datas ): return np.array([np.argmin(((np.tile(data,(k,1 ))-center)**2 ).sum (axis=1 )) for data in datas])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 k=4 min_loss=10000 min_loss_center=np.array([]) min_loss_result=np.array([]) for i in range (50 ): center,resultData=kmeans(data,k) loss=sum (resultData[:,1 ])/data.shape[0 ] if loss<min_loss: min_loss=loss min_loss_center=center min_loss_result=resultData center=min_loss_center resultData=min_loss_result showCluster(data,k,center,resultData)
1 2 3 4 5 6 7 8 9 10 11 12 x_min, x_max = data[:, 0 ].min () - 1 , data[:, 0 ].max () + 1 y_min, y_max = data[:, 1 ].min () - 1 , data[:, 1 ].max () + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02 ), np.arange(y_min, y_max, 0.02 )) z = predict(np.c_[xx.ravel(), yy.ravel()]) z=z.reshape(xx.shape) cs=plt.contourf(xx,yy,z) showCluster(data,k,center,resultData)
在经过多次循环取得损失最小时对应的重心和结果时,多次运行聚类的结果明显比较稳定了许多
2.K值选取是由用户决定的,不同k值得到的结果会有很大的不同
1 2 3 import numpy as npimport matplotlib.pylab as pltdata=np.genfromtxt('kmeans.txt' ,delimiter=' ' )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 def eucldistance (v1,v2 ): return np.sqrt(sum ((v2-v1)**2 )) def initCenter (data,k ): numSanples,dim=data.shape center=np.zeros((k,dim)) for i in range (k): index=int (np.random.uniform(0 ,numSanples)) center[i,:]=data[index,:] return center def kmeans (data,k ): numSamples=data.shape[0 ] resultData=np.array(np.zeros((numSamples,2 ))) isChange=True center=initCenter(data,k) while (isChange): isChange=False for i in range (numSamples): Mindist=10000 minindex=0 for j in range (k): distance=eucldistance(center[j,:],data[i,:]) if (distance<Mindist): Mindist=distance resultData[i,1 ]=distance minindex=j if resultData[i,0 ] !=minindex: isChange=True resultData[i,0 ]=minindex for j in range (k): cluster_index=np.nonzero(resultData[:,0 ]==j) point=data[cluster_index] center[j,:]=np.mean(point,axis=0 ) return center,resultData
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 def showCluster (data, k, centroids, resultData ): numSamples, dim = data.shape if dim != 2 : print ("dimension of your data is not 2!" ) return 1 mark = ['or' , 'ob' , 'og' , 'ok' , '^r' , '+r' , 'sr' , 'dr' , '<r' , 'pr' ] if k > len (mark): print ("Your k is too large!" ) return 1 for i in range (numSamples): markIndex = int (resultData[i, 0 ]) plt.plot(data[i, 0 ], data[i, 1 ], mark[markIndex]) mark = ['*r' , '*b' , '*g' , '*k' , '^b' , '+b' , 'sb' , 'db' , '<b' , 'pb' ] for i in range (k): plt.plot(centroids[i, 0 ], centroids[i, 1 ], mark[i], markersize = 20 ) plt.show() def predict (datas ): return np.array([np.argmin(((np.tile(data,(k,1 ))-center)**2 ).sum (axis=1 )) for data in datas])
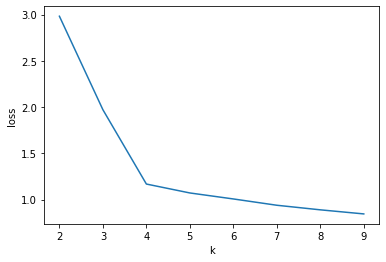
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 list_lost=[] for k in range (2 ,10 ): min_loss=10000 min_loss_center=np.array([]) min_loss_result=np.array([]) for i in range (50 ): center,resultData=kmeans(data,k) loss=sum (resultData[:,1 ])/data.shape[0 ] if loss<min_loss: min_loss=loss min_loss_center=center min_loss_result=resultData list_lost.append(min_loss)
[2.9811811738953176,
1.9708559728104191,
1.1675654672086735,
1.0712368269135584,
1.0064227003008,
0.9383457643136094,
0.8888370860975188,
0.8447057982645164]
1 2 3 4 plt.plot(range (2 ,10 ),list_lost) plt.xlabel('k' ) plt.ylabel('loss' ) plt.show()
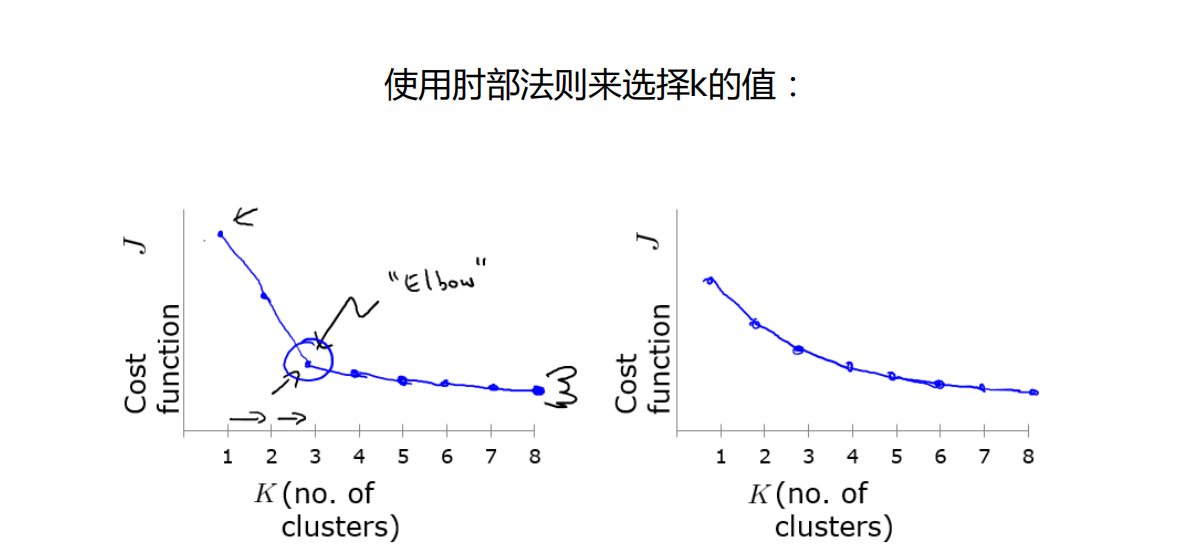
从图中可以明显看出k=4时就是其肘部点,将该样本数据聚成4类较为合理
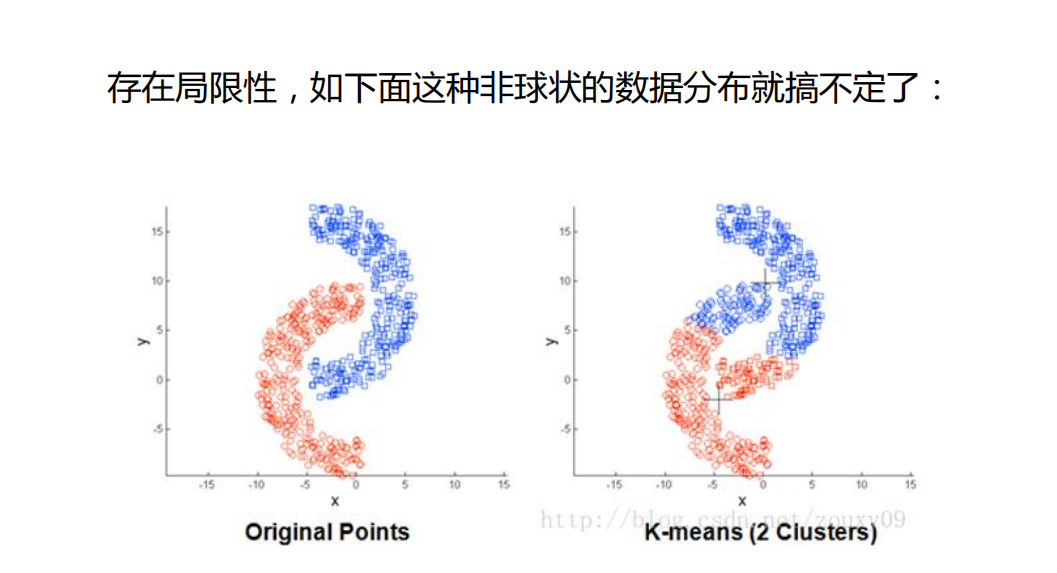
3.存在局限性
4.数据比较大的时候,收敛会比较慢
解决办法:mini batch k-means
4.DBSCan算法
DBSCAN算法算法是基于密度得一类聚类算法,可以将具有足够高密度的区域划分成簇,并可以发现任何形状的聚类。ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ ϵ \epsilon ϵ
算法思想
1.指定合适的ϵ \epsilon ϵ ϵ \epsilon ϵ
算法优缺点:ϵ \epsilon ϵ
算法可视化网站 ,有兴趣可以去玩一玩。
sklearn实现
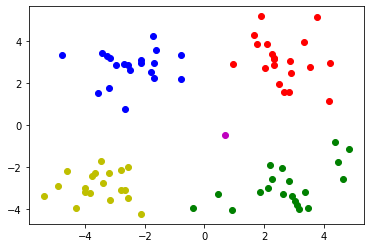
1 2 3 from sklearn.cluster import DBSCANimport numpy as npimport matplotlib.pyplot as plt
1 2 data=np.genfromtxt('kmeans.txt' ,delimiter=' ' )
1 2 3 4 model=DBSCAN(eps=1.5 ,min_samples=4 ) model.fit(data)
DBSCAN(eps=1.5, min_samples=4)
1 2 3 result=model.fit_predict(data) result
array([ 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, -1, 2, 0,
1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1,
2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2,
3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,
0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3], dtype=int64)
1 2 3 4 5 6 mark=['or' ,'ob' ,'og' ,'oy' ,'ok' ,'om' ] for i ,d in enumerate (data): plt.plot(d[0 ],d[1 ],mark[result[i]]) plt.show()