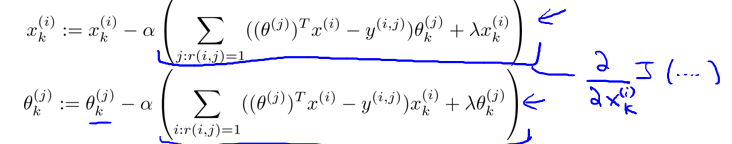问题引入
假设我们是一个电影供应商,我们有5部电影和4个用户,我们要求用户为电影打分。
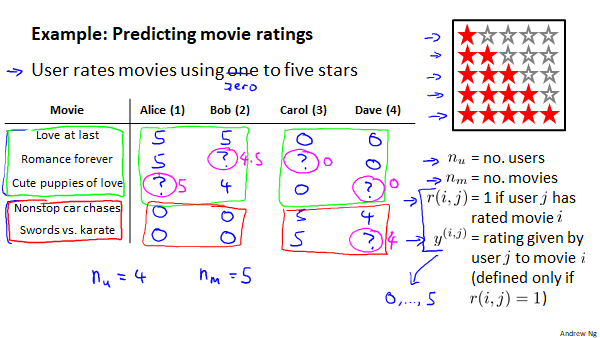
电影中前3部为爱情片,后两部则是动作片,我们可以从表中数据看出Alice和Bob更喜欢爱情片,而Carol和Dave更倾向于动作片。没有一个用户给所有电影打过分,我们希望构建一个算法来预测他们每个人可能会给他们没看过的电影打分,并以此作为推荐的依据。
下面我们下引入一些标记:
nu代表用户的数量
nm代表电影的数量
r(i,j)=1表示用户j给电影i评过分,如果为0则没有
y(i,j)表示用户给电影的i的评分
mj 表示用户j评过分的电影的总数
基于内容的推荐系统

如图所示,我们假设每部电影都有两个特征,用x1代表电影的浪漫程度,用x2代表电影的动作程度。则每部电影都有一个特征向量,如第一部电影的特征向量为x1=[1,0.9,0](加上截距x0=1).
下面我们要根据这些特征来构建一个推荐系统算法。我们采用线性回归模型,对每一个用户都训练一个线性回归模型,以此来预测用户的打分情况,
假设第一个用户的参数向量为θ(1)=[0,5,0]则其对第三部电影的评分预测为(θ(1))Tx(3)=4.95我们用θ(1)来表示她对电影评分中爱情成分和动作成分所占的影响。
所以为了学习这个θ,我们采用线性回归的方法来求解。
所以我们可就构造代价函数:
min(θ(j))2m(j)1i:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2m(j)λk=1∑n(θk(j))2
为了简化计算,我们将m去掉得:
min(θ(j))21i:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λk=1∑n(θk(j))2
这是一个用户的,所有用户的可写作:
min(θ(1),θ(2)...θnu)21j=1∑nui:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
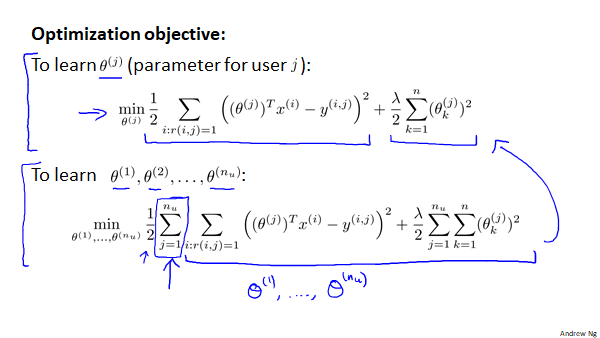
其中:
θ(j)表示用户j的参数向量
x(i)表示电影i的特征向量。
对于用户j和电影i我们的预测评分为((θ(j))Tx(i))
接下来就是采用梯度下降法来最小化代价函数求解θ:

协同过滤
在基于内容的推荐系统中,对于每一部电影,我们都有其特征,通过这些特征训练出每一个用户的线性回归参数。那么这些特征是从何而来呢,与之相反如果我们用于用户的模型参数,那么我们也可以通过同样的方法学习出每部电影的特征。
min(x(1),x(2)...xnm)21i=1∑nmj:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λi=1∑nmk=1∑n(xk(j))2
那么问题又来了,用户的模型参数是通过电影的特征向量算出来的,而知道用户的模型参数才可以计算电影的特征,这就类似于鸡和蛋的问题了,如果两者的特征都没有,以上两种方法都无法完成计算了。而协调过滤算法则可以同时学习用户的模型参数和电影的特征。
首先我们将上面两种方法的代价函数结合为一个:
min(θ(1),θ(2)...θnu)21j=1∑nui:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
min(x(1),x(2)...xnm)21i=1∑nmj:r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λi=1∑nmk=1∑n(xk(j))2
第一个式子的求和运算是对所以用户求和,将每个用户对其打过分的电影的分值误差相加。而第二个则是与第一个加和顺序相反,对每部电影求和。而这虽然形式不同,但其计算的内容都是一样的,都是对r(i,j)=1的部分进行求和,因而这两个式子合并为下边的这个样子。
J((x(1),x(2)...xnm),(θ(1),θ(2)...θnu))=21(i,j):r(i,j)=1∑((θ(j))T(x(i))−y(i,j))2+2λi=1∑nmk=1∑n(xk(j))2+2λj=1∑nuk=1∑n(θk(j))2

接着对x和θ同时进行更新,分别对代价函数求偏导并应用梯度下降法得:
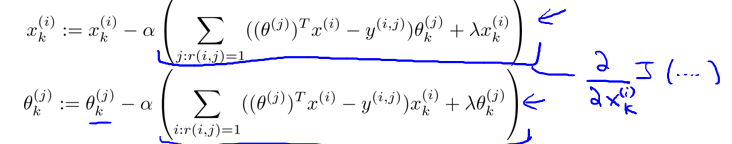
协调过滤得步骤为:
1.初始化x(1),x(2),...x(nm),θ(1),θ(2),...θ(nu)为一些随机小值
2.使用梯度下降法最小化代价函数
3.在训练玩算法后,预测(θ(j))Tx(i)即为用户j给电影i得评分。
实现
1
2
| import numpy as np
import matplotlib.pyplot as plt
|
1
2
3
4
5
6
7
8
9
10
| nu=4
nm=5
n=3
Y=np.array([[5,5,0,0],
[5,-1,-1,0],
[-1,4,0,-1],
[0,0,5,4],
[0,0,5,-1]])
Y
|
array([[ 5, 5, 0, 0],
[ 5, -1, -1, 0],
[-1, 4, 0, -1],
[ 0, 0, 5, 4],
[ 0, 0, 5, -1]])
1
2
3
4
5
| R=np.ones((nm,nu))
print(Y==-1)
idx=np.nonzero(Y==-1)
R[idx]=0
R
|
[[False False False False]
[False True True False]
[ True False False True]
[False False False False]
[False False False True]]
array([[1., 1., 1., 1.],
[1., 0., 0., 1.],
[0., 1., 1., 0.],
[1., 1., 1., 1.],
[1., 1., 1., 0.]])
1
2
3
4
5
6
| lambda1=0.1
alpha=0.0001
x=np.random.rand(nm,n)
theta=np.random.rand(nu,n)
print(x)
print(theta)
|
[[0.82558579 0.39527941 0.37386907]
[0.58716221 0.46424579 0.46917673]
[0.44178532 0.50338717 0.61866128]
[0.25719809 0.70487604 0.31728937]
[0.22616126 0.81379085 0.14697015]]
[[0.70964616 0.5690154 0.5058206 ]
[0.46830044 0.74712758 0.1572838 ]
[0.4588972 0.97639083 0.08482318]
[0.72948113 0.90433426 0.32549155]]
1
2
3
4
5
| J=0
J_list=[]
x_grad=np.zeros((x.shape))
theta_grad=np.zeros((theta.shape))
theta_grad
|
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
1
2
3
4
| a = np.array([[1, 2], [3, 4]], dtype=np.int32)
b = np.array([[5, 6], [7, 8]], dtype=np.int32)
a.dot(b).shape
a**2
|
array([[ 1, 4],
[ 9, 16]], dtype=int32)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
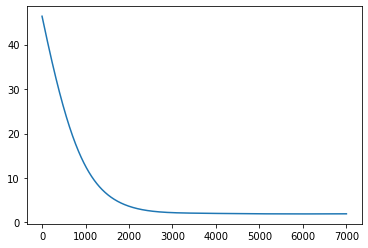
| epochs=7000
for i in range(epochs+1):
predict=x.dot(theta.T)*R
x_grad=((predict-Y)).dot(theta)+lambda1*x
theta_grad=(predict-Y).T.dot(x)+lambda1*theta
x=x-alpha*x_grad
theta=theta-alpha*theta_grad
if(i%10==0):
J=0.5*np.sum(sum(predict-Y)**2)+0.5*lambda1*sum((sum(theta**2)))+0.5*lambda1*sum(sum(x**2))
J_list.append(J)
epochs_list=np.linspace(0,7001,701)
plt.plot(epochs_list,J_list)
J_list[-1]
|
1.9252136083530944
1
2
| predict=x.dot(theta.T)
predict
|
array([[ 5.09769368e+00, 4.79217330e+00, -2.80955385e-01,
3.07809666e-01],
[ 4.06274711e+00, 3.62314012e+00, -3.09562410e+00,
-1.16908398e+00],
[ 2.83958627e+00, 2.71017075e+00, -4.70002243e-01,
-3.32168008e-03],
[-1.77998169e-01, 2.82910243e-01, 5.59091874e+00,
2.71547237e+00],
[-2.27366856e-01, 1.44788586e-01, 4.47887027e+00,
2.16854026e+00]])