降维

 当我们处理待处理样本数据的特征过多，而其中有些特征有有些重复，计算起来速度较慢，我们可以采用降维算法。 假使我们要采用两种不的仪器来测量一些东西的尺寸，其中一个仪器测量结果的单位是英寸，另一个仪器测量的结果是厘米，我们希望将测量的结果作为我们机器学习的特征。现在的问题的是，两种仪器对同一个东西测量的结果不完全相等（由于误差、精度等），而将两者都作为特征有些重复，因而，我们希望将这个二维的数据降至一维.将数据从二维降至一维的过程就叫做降维。
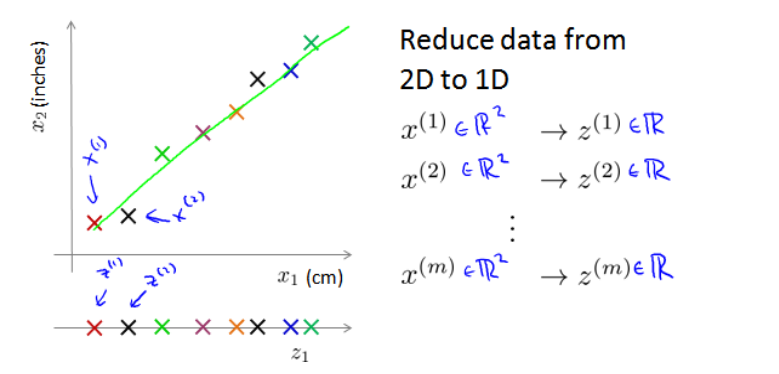
20220130114733
如图所示，将所有在一个平面上的样本点转换到一条直线上，将一组两维的数据用一组一维的来表示，这就是将二维数据降为一维。
而对于三维的数据我们可以降维两维，将所有的样本点投影至一个平面。
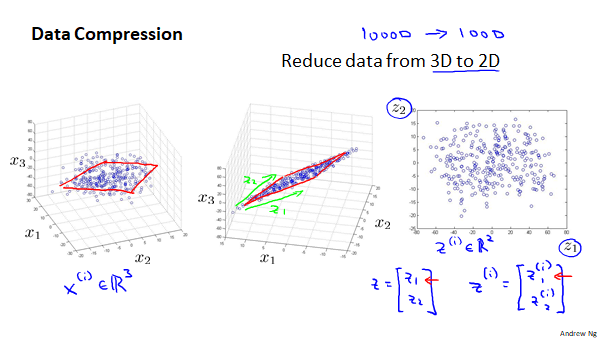
20220130115449

为什么要降维

数据压缩

数据压缩可以使用较少的计算机内存或磁盘空间，同时也可以加速我们的学习算法。对于一些特征数量较高的样本数据，如果不进行数据压缩，计算量会非常的大，学习的速度太慢。

数据可视化

在许多机器学习问题中，如果我们能将数据可视化，我们就有可能寻找到一个更好的解决方案。这时候就用到了降维。
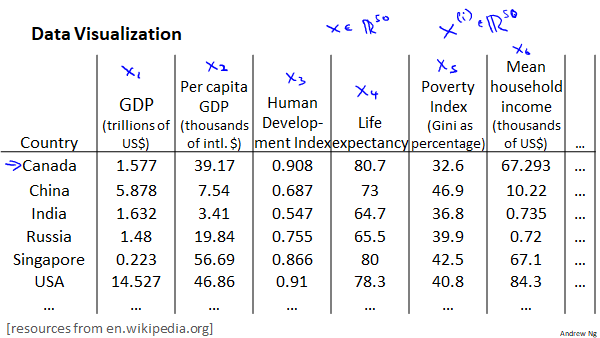
20220130115842
假设我们有许多关于不同国家的数据，每个特征向量都有50个特征，如果要将这50维数据可视化是不可能的的，如果我们能通过降维的方法将其降至2维，就可以进行可视化了。

主成成分分析(PCA)算法

主成成分分析(Principal components analysis 简称PCA)是最重要的的降维方法之一。。PCA算法要做的就是找出数据里面的主要的方面，用其来代替原始的数据。在PCA中，我们要做的就是找到一个方向向量，当把所有的数据都投射到该向量上时，我们希望投射的平均均方误差尽可能的小。
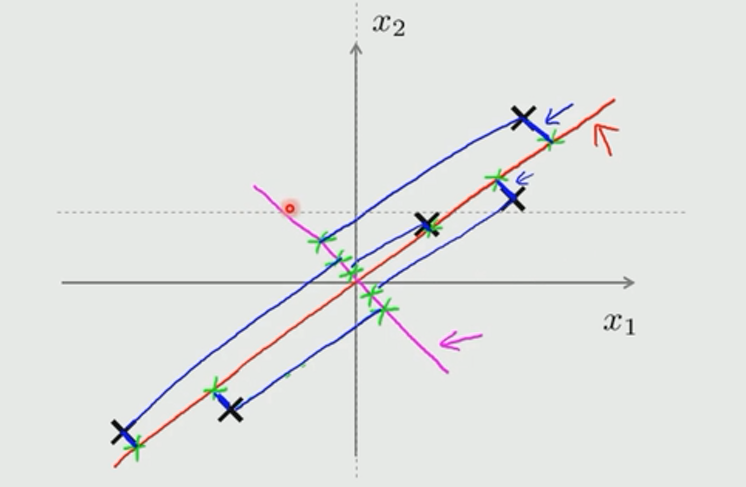
20220130120952
在图中所示的数据中，我们选择红色的线作为方向向量，而不选择粉红色的线就是应为其平均均方误差小。

PCA与线性回归的区别

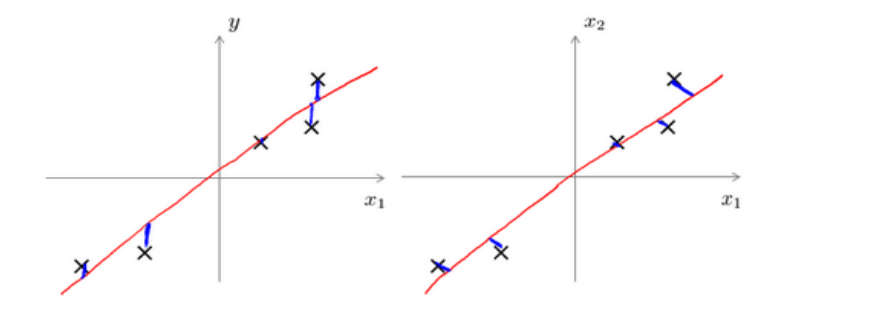
20220130121235
如图所示，左边是线性回归的误差(垂直于横轴方向)，线性回归尝试最小化的是预测误差，来预测结果；右边是PCA的误差，垂直于方向向量，最小化的是投射误差，并不会做任何预测。

PCA算法流程

1.数据预处理：中心化X-x‾\overline{x}
2.求样本的协方差矩阵1mXXT\frac{1}{m}XX^{T}
3.对协方差1mXXT\frac{1}{m}XX^{T}矩阵做特征值分解。
4.选出最大的k个特征值对于的k个特征向量
5.将原始数据投影到选取的特征向量上。
6.输出投影后的数据集。
证明过程看不太懂😭，所以这里仅给出算法流程，具体证明过程可以去看下面这篇博客：主成分分析（PCA）原理总结

PCA实现

python实现
1
2
import numpy as np
import matplotlib.pylab as plt
1
2
3
4
5
6
7
#载入数据
data=np.genfromtxt('data.csv',delimiter=',')
x_data=data[:,0]
y_data=data[:,1]
plt.scatter(x_data,y_data)
plt.show()
data.shape

​
png
​

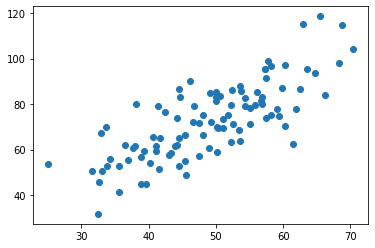
(100, 2)

1
2
3
4
5
6
#去中心化
def zeroMean(dataMat):
    #按列求各个特征的平均值
    meanMaT=np.mean(dataMat,axis=0)
    newMat=dataMat-meanMaT
    return newMat,meanMaT
1
2
3
4
newMat,meanMat=zeroMean(data)
#np.cov 用于求协方差矩阵，参数rowvar说明数据一行代表一个样本
covMat=np.cov(newMat,rowvar=0)
covMat#协方差矩阵
array([[ 94.99190951, 125.62024804],
       [125.62024804, 277.49520751]])

1
2
#也可以用 (X.T * X)/m直接来算
newMat.T.dot(newMat)/newMat.shape[0]
array([[ 94.04199041, 124.36404556],
       [124.36404556, 274.72025544]])

1
2
#np.linalg.eig求矩阵特征值和特征向量
eigVal,eigVects=np.linalg.eig(np.mat(covMat))
1
2
#特征值
eigVal
array([ 30.97826888, 341.50884814])

1
2
#特征向量
eigVects
matrix([[-0.89098665, -0.45402951],
        [ 0.45402951, -0.89098665]])

1
2
3
#对特征值从小到大排序
eigValIndex=np.argsort(eigVal)
eigValIndex
array([0, 1], dtype=int64)

1
2
3
4
k=1 #降为k维
n_eigValIndex=eigValIndex[-1:-(k+1):-1]
#最后一个-1是代表从右向左取数
n_eigValIndex
array([1], dtype=int64)

1
2
3
#最大的n个特征值所对应的特征向量
n_eigVect=eigVects[:,n_eigValIndex]
n_eigVect
matrix([[-0.45402951],
        [-0.89098665]])

1
2
3
#降维后的数据
lowdata=newMat*n_eigVect
lowdata[:5,:]
matrix([[ 44.02694787],
        [  1.49722533],
        [  3.35564513],
        [  1.73205523],
        [-17.84406034]])

1
2
3
#用低纬度数据来重构数据
recoMat=(lowdata*n_eigVect.T)+meanMat
recoMat[:5,:]
matrix([[28.96880808, 33.50762783],
        [48.27855698, 71.40104277],
        [47.43477956, 69.74521555],
        [48.17193728, 71.19181247],
        [57.06007136, 88.63387007]])

1
2
3
plt.scatter(x_data,y_data)
plt.scatter(np.array(recoMat)[:,0],np.array(recoMat)[:,1],c='r')
plt.show()

png

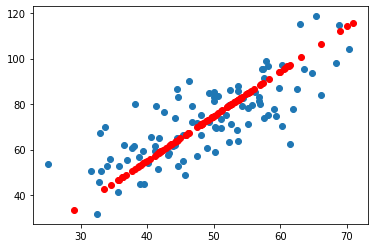
sklearn实现
1
2
3
from sklearn.decomposition import PCA
model=PCA(n_components=1)#n_components 表示降维后的维数
model.fit(data)
PCA(n_components=1)

1
model.explained_variance_#特征值
array([341.50884814])

1
model.explained_variance_ratio_#所保留的n个成分各自的方差百分比
1
array([0.91683399])
1
model.components_#特征向量
array([[0.45402951, 0.89098665]])

1
2
new_data=model.transform(data)#降维后的数据
new_data[:5,:]
array([[-44.02694787],
       [ -1.49722533],
       [ -3.35564513],
       [ -1.73205523],
       [ 17.84406034]])

1
2
3
4
recdata=model.inverse_transform(new_data)#将降维后的数据还原
plt.scatter(data[:,0],data[:,1])
plt.scatter(recdata[:,0],recdata[:,1],c='r')
plt.show()

png

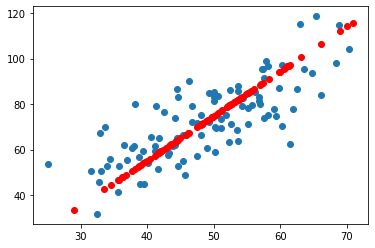
PCA算法优缺点

优点

1.仅仅需要以方差衡量信息量，不受数据集以外的因素影响
2.各主成成分之间正交，可以消除原始数据成分间的相互影响的因素
3.计算方法简单，主要运算是特征值分解，易于实现

缺点

1.主成成分各个特征维度的含义具有一定的模糊性，不如原始样本解释性强
2.方差小的非主成成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响