后面原文件内容来自datawhalechina/powerful-numpy: 巨硬的NumPy (github.com)

基本操作

这部分是在看下面的教程中，自己跟着写的一些代码。如果学习的化直接看第二部分。

导包

1	import numpy as np

从列表或元组中创建

1
2
3

a=np.array([1,2,3])#一维
print(a)

[1 2 3]

使用arange生成

b=np.array(range(1,6))
print(b)
c=np.arange(1,6)
print(c)
d=np.arange(1,6,2)#2为步长
print(d)

1
2
3

[1 2 3 4 5]
[1 2 3 4 5]
[1 3 5]

使用linespace/logspace生成

1	np.linspace(0,9,10)#开头，结尾，数量

array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

1	np.linspace(0,9,7)#是一种线性的等差数列

array([0. , 1.5, 3. , 4.5, 6. , 7.5, 9. ])

1	np.logspace(0,9,6,base=np.e)#需要额外添加一个base，默认为10

array([1.00000000e+00, 6.04964746e+00, 3.65982344e+01, 2.21406416e+02,
       1.33943076e+03, 8.10308393e+03])

数组形状

.shape来查看数组形状
reshape 修改数组形状

import numpy as np
>>> t1=np.arange(1,13)
>>> t1
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])
>>> t1.shape#一维数组
(12,)
>>> t2=np.array([[1,2,3],[4,5,6]])
>>> t2
array([[1, 2, 3],
       [4, 5, 6]])
>>> t2.shape#二维数组
(2, 3)

>>> t1
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])
>>> t1.reshape((3,4))#将t1转换为3行4列的数组
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
>>> t1.reshape((3,-1))#-1表示自动计算每行应该有多少列
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
>>> t1
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])
>>> t1.reshape((-1,1))#将数组转换为一列
array([[ 1],
       [ 2],
       [ 3],
       [ 4],
       [ 5],
       [ 6],
       [ 7],
       [ 8],
       [ 9],
       [10],
       [11],
       [12]])

one/zeros创建

1	np.ones(3)

array([1., 1., 1.])

1	np.ones((2,3))

array([[1., 1., 1.],
       [1., 1., 1.]])

1	np.zeros((3,2))

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

#np.zeros_like 或 np.ones_like，二者可以快速生成给定 array 一样 shape 的 0 或 1 向量
a=np.array([[1,2],[2,3]])
print(np.zeros_like(a))
np.ones_like(a)

[[0 0]
 [0 0]]





array([[1, 1],
       [1, 1]])

使用random生成

1 2	#0-1均匀分布 np.random.rand(2,3)

1 2	array([[0.42926805, 0.43072106, 0.53702462], [0.89851387, 0.18539595, 0.42793225]])

1 2	#单个数 np.random.rand()

0.36071062769229123

1 2	#指定上下界的均匀分布 np.random.uniform(-1,1,(2,3))

array([[-0.64544541, -0.25383872, 0.1808275 ],
[-0.43496897, -0.80391586, 0.06209736]])

1
2
3

#通过 np.random.default_rng() 先生成 Generator，然后再在此基础上生成各种分布的数据（记忆更加简便清晰）。
rng=np.random.default_rng(1)#1是种子
rng

1	Generator(PCG64) at 0x22AEFEE74A0

1	rng.random((2,3))#均匀分布

1 2	array([[0.51182162, 0.9504637 , 0.14415961], [0.94864945, 0.31183145, 0.42332645]])

1	rng.uniform(-1,1,(3,2))#指定上下界的均匀分布

 array([[ 0.65540519, -0.18160173],
        [ 0.09918738, -0.94488177],
        [ 0.50702622,  0.07628663]])

1 2	# 随机整数（离散均匀分布），不超过给定的值（10） np.random.randint(10, size=2)

 array([1, 2])

1 2	# 随机整数（离散均匀分布），指定上下界和 shape np.random.randint(0, 10, (2, 3))

 array([[8, 9, 1],
        [2, 6, 1]])

1 2	#标准正态分布 np.random.rand(2,4)

1 2	array([[0.13697705, 0.16495722, 0.7386519 , 0.30595425], [0.53560286, 0.06430746, 0.90285721, 0.47987077]])

1 2	#高斯分布 np.random.normal(0,1,(3,4))

 array([[ 1.12032801, -0.89480603,  0.90740065,  1.72309526],
        [ 0.11032696,  0.15336619, -0.60820831, -0.08424255],
        [-0.29166234, -0.80346217,  0.48008174,  0.7266655 ]])

求平均值和标准差

1 2	arr=np.array([[1,2,3],[4,5,6],[7,8,9]]) np.average(arr)#求平均值

5.0

1	np.average(arr,axis=0)#按列求平均

array([4., 5., 6.])

1	np.average(arr,axis=1)#按行求平均

array([2., 5., 8.])

1	arr.sum(axis=1)#按行求和

array([ 6, 15, 24])

1	np.sum(arr,axis=0)#按列求和

array([12, 15, 18])

1	np.mean(arr)#另一种求平均值

5.0

1	np.std(arr)#标准差

2.581988897471611

1	np.var(arr)#方差标准差和方差用法与平均值的类似，都可以按行或按列求和

6.666666666666667

反序和转置

1
2
3

#字符串
s="abcdef"
s[::-1]

'fedcba'

1
2
3

#数组
list=[1,2,3,4]
list[::-1]

[4, 3, 2, 1]

arr

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr.T

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

分解和组合

1 2	a=np.random.rand(3,4) a

array([[0.28316861, 0.76199416, 0.91081204, 0.19720986],
       [0.50787399, 0.78146294, 0.60943133, 0.93976186],
       [0.55123214, 0.60483931, 0.36117639, 0.38412533]])

1
2
3

b=np.ones((a.shape[0],1))
c=np.ones((1,a.shape[1]))
print(b,c)

[[1.]
 [1.]
 [1.]] [[1. 1. 1. 1.]]

1 2	#默认axis=0 按列拼接 np.concatenate((a,c))

array([[0.28316861, 0.76199416, 0.91081204, 0.19720986],
       [0.50787399, 0.78146294, 0.60943133, 0.93976186],
       [0.55123214, 0.60483931, 0.36117639, 0.38412533],
       [1.        , 1.        , 1.        , 1.        ]])

1	np.concatenate((a,b),axis=1)#按行拼接

array([[0.28316861, 0.76199416, 0.91081204, 0.19720986, 1.        ],
       [0.50787399, 0.78146294, 0.60943133, 0.93976186, 1.        ],
       [0.55123214, 0.60483931, 0.36117639, 0.38412533, 1.        ]])

拆分

1
2
3

#拆分
arr=np.random.rand(4,3)
arr

array([[0.83040698, 0.86874681, 0.32073868],
       [0.84843869, 0.94233061, 0.57501876],
       [0.34525372, 0.9804726 , 0.11702269],
       [0.75533314, 0.97914285, 0.10175191]])

1	np.split(arr,4)#默认axis=0按列切分

[array([[0.83040698, 0.86874681, 0.32073868]]),
 array([[0.84843869, 0.94233061, 0.57501876]]),
 array([[0.34525372, 0.9804726 , 0.11702269]]),
 array([[0.75533314, 0.97914285, 0.10175191]])]

筛选和过滤

1
2
3

#筛选和过滤
arr=np.random.randint(1,100,(3,4))
arr

array([[44, 83, 40, 85],
       [70, 96, 22, 78],
       [71, 24, 87, 59]])

1	arr>60#条件筛选

array([[False,  True, False,  True],
       [ True,  True, False,  True],
       [ True, False,  True, False]])

1 2	np.where(arr>60)# ## 返回满足条件的索引，因为是两个维度，所以会返回两组结果

(array([0, 0, 1, 1, 1, 2, 2], dtype=int64),
 array([1, 3, 0, 1, 3, 0, 2], dtype=int64))

1 2	# 不满足条件的赋值，将 <=60 的替换为 -1 np.where(arr > 60, arr, -1)

array([[-1, 83, -1, 85],
       [70, 96, -1, 78],
       [71, -1, 87, -1]])

1 2	#np.nonzero 可以起到与where相同的作用 np.nonzero(arr>60)

(array([0, 0, 1, 1, 1, 2, 2], dtype=int64),
 array([1, 3, 0, 1, 3, 0, 2], dtype=int64))

1
2
3

index=np.nonzero(arr>60)
arr[index]=1#大于60的设置为1
arr

array([[44,  1, 40,  1],
       [ 1,  1, 22,  1],
       [ 1, 24,  1, 59]])

最值索引

1
2
3

## 最值索引
arr=np.random.uniform(1,100,(4,3))
arr

array([[97.8734874 , 39.23597617, 37.72185051],
       [47.83484032, 27.14324385, 70.51344464],
       [68.39641974, 68.26842052, 26.72485587],
       [72.27555183, 46.34734565, 12.28779778]])

1	np.argmax(arr)#返回最大值的index

1	np.argmax(arr,axis=0)#按列

array([0, 2, 1], dtype=int64)

1	np.argmax(arr,axis=1)#按行

array([0, 2, 0, 0], dtype=int64)

1	np.argsort(arr)#默认axis=1按行排序

array([[2, 1, 0],
       [1, 0, 2],
       [2, 1, 0],
       [2, 1, 0]], dtype=int64)

1	np.argsort(arr,axis=0)#按列

array([[1, 1, 3],
       [2, 0, 2],
       [3, 3, 0],
       [0, 2, 1]], dtype=int64)

矩阵运算

1 2	arr=np.array([[1,2,3],[4,5,6],[7,8,9]]) arr

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

1	arr2#+-/都是对每个数都进行运算

array([[ 2,  4,  6],
       [ 8, 10, 12],
       [14, 16, 18]])

arr**3#立方

array([[  1,   8,  27],
       [ 64, 125, 216],
       [343, 512, 729]], dtype=int32)

1	np.sqrt(arr)#开方

array([[1.        , 1.41421356, 1.73205081],
       [2.        , 2.23606798, 2.44948974],
       [2.64575131, 2.82842712, 3.        ]])

1	np.log(arr)#log

array([[0.        , 0.69314718, 1.09861229],
       [1.38629436, 1.60943791, 1.79175947],
       [1.94591015, 2.07944154, 2.19722458]])

1	np.mod(arr,3)#模运算

array([[1, 2, 0],
       [1, 2, 0],
       [1, 2, 0]], dtype=int32)

矩阵乘法

1
2
3

a=np.array([[1,2],[3,4],[5,6]])
b=np.array([[1,2,3,4],[5,6,7,8]])
c=np.array([[1,2,3],[4,5,6],[7,8,9]])

1 2	#矩阵乘法 np.dot(a,b)

array([[11, 14, 17, 20],
       [23, 30, 37, 44],
       [35, 46, 57, 68]])

1	a@b#等同于.dot

array([[11, 14, 17, 20],
       [23, 30, 37, 44],
       [35, 46, 57, 68]])

a*a#点乘

array([[ 1,  4],
       [ 9, 16],
       [25, 36]])

1 2	print(np.vdot(a,a))#点积 np.sum(a*a)

91

91

原文件

这篇教程是从Github上的，源地址datawhalechina/powerful-numpy: 巨硬的NumPy (github.com)，由于ipynb文件在线阅读不方便，就转换成了markdown文件放在这里了，决定写的不错的可以到项目底下点点star支持一下作者。

在学习numpy是把这些代码看一下就行了，用的时候直接查就行了，用多了自然就会了。

本教程内容旨在帮助没有基础的同学快速掌握 numpy 的常用功能，保证日常绝大多数场景的使用。可作为机器学习或深度学习的先修课程，也可作为快速备查手册。

值得一提的是，深度学习的各大框架很多 API 和 numpy 也是一脉相承的哦，可以说 numpy 玩儿熟了，几个深度学习框架的不少 API 也同时学会了。

教程原则如下：

偏实用高频 API
展示实际用法
简单直接

使用说明如下：

每一小节都有⭐（1-5个）表示重要程度，越多越重要
每一小节下重要的会单独列成一个更小的小节，可以通过目录直接访问。其中分割线下面的可以补充了解
⚠️ 表示需要特别注意的

特别需要提醒的是，您在使用的过程中无须过多关注 API 各种参数细节，教程提供的用法足以应付绝大部分场景，更深入的使用方式可以自行根据需要探索或学习后续的《基础教程》。

# 导入 library
import numpy as np
# 画图工具
import matplotlib.pyplot as plt

创建和生成

本节主要介绍 array 的创建和生成。为什么会把这个放在最前面呢？主要有以下两个方面原因：

在实际工作过程中，我们时不时需要验证或查看 array 相关的 API 或互操作。
有时候在使用 sklearn，matplotlib，PyTorch，Tensorflow 等工具时也需要一些简单的数据进行实验。

所以，先学会如何快速拿到一个 array 是有很多益处的。本节我们主要介绍以下几种常用的创建方式：

使用列表或元组
使用 arange
使用 linspace/logspace
使用 ones/zeros
使用 random
从文件读取

其中，最常用的一般是 linspace/logspace 和 random，前者常常用在画坐标轴上，后者则用于生成「模拟数据」。举例来说，当我们需要画一个函数的图像时，X 往往使用 linspace 生成，然后使用函数公式求得 Y，再 plot；当我们需要构造一些输入（比如 X）或中间输入（比如 Embedding、hidden state）时，random 会异常方便。

从 python 列表或元组创建

⭐⭐ 重点掌握传入 list 创建一个 array 即可：np.array(list)

⚠️ 需要注意的是：「数据类型」。如果您足够仔细的话，可以发现下面第二组代码第 2 个数字是「小数」（注：Python 中 1. == 1.0），而 array 是要保证每个元素类型相同的，所以会帮您把 array 转为一个 float 的类型。

1 2	# 一个 list np.array([1,2,3])

array([1, 2, 3])

1
2
3

# 二维（多维类似）
# 注意，有一个小数哦
np.array([[1, 2., 3], [4, 5, 6]])

array([[1., 2., 3.],
       [4., 5., 6.]])

1 2	# 您也可以指定数据类型 np.array([1, 2, 3], dtype=np.float16)

array([1., 2., 3.], dtype=float16)

# 如果指定了 dtype，输入的值都会被转为对应的类型，而且不会四舍五入
lst = [
    [1, 2, 3],
    [4, 5, 6.8]
]
np.array(lst, dtype=np.int32)

array([[1, 2, 3],
       [4, 5, 6]], dtype=int32)

1 2	# 一个 tuple np.array((1.1, 2.2))

array([1.1, 2.2])

1 2	# tuple，一般用 list 就好，不需要使用 tuple np.array([(1.1, 2.2, 3.3), (4.4, 5.5, 6.6)])

array([[1.1, 2.2, 3.3],
       [4.4, 5.5, 6.6]])

1 2	# 转换而不是上面的创建，其实是类似的，无须过于纠结 np.asarray((1,2,3))

array([1, 2, 3])

1	np.asarray(([1., 2., 3.], (4., 5., 6.)))

array([[1., 2., 3.],
       [4., 5., 6.]])

使用 arange 生成

⭐⭐

range 是 Python 内置的整数序列生成器，arange 是 numpy 的，效果类似，会生成一维的向量。我们偶尔会需要使用这种方式来构造 array，比如：

需要创建一个连续一维向量作为输入（比如编码位置时可以使用）
需要观察筛选、抽样的结果时，有序的 array 一般更加容易观察

⚠️ 需要注意的是：在 reshape 时，目标的 shape 需要的元素数量一定要和原始的元素数量相等。

1	np.arange(12).reshape(3, 4)

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

1 2	# 注意，是小数哦 np.arange(12.0).reshape(4, 3)

array([[ 0.,  1.,  2.],
       [ 3.,  4.,  5.],
       [ 6.,  7.,  8.],
       [ 9., 10., 11.]])

1	np.arange(100, 124, 2).reshape(3, 2, 2)

array([[[100, 102],
        [104, 106]],

       [[108, 110],
        [112, 114]],

       [[116, 118],
        [120, 122]]])

1 2	# shape size 相乘要和生成的元素数量一致 np.arange(100., 124., 2).reshape(2,3,4)

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-20-fc850bf3c646> in <module>
----> 1 np.arange(100., 124., 2).reshape(2,3,4)


ValueError: cannot reshape array of size 12 into shape (2,3,4)

使用 linspace/logspace 生成

⭐⭐⭐

OK，这是我们遇到的第一个比较重要的 API，前者需要传入 3 个参数：开头，结尾，数量；后者需要额外传入一个 base，它默认是 10。

⚠️ 需要注意的是：第三个参数并不是步长。

`np.linspace`

1 2	# 线性 np.linspace(0, 9, 10).reshape(2, 5)

array([[0., 1., 2., 3., 4.],
       [5., 6., 7., 8., 9.]])

1	np.linspace(0, 9, 6).reshape(2, 3)

array([[0. , 1.8, 3.6],
       [5.4, 7.2, 9. ]])

1 2	# 指数 base 默认为 10 np.logspace(0, 9, 6, base=np.e).reshape(2, 3)

array([[1.00000000e+00, 6.04964746e+00, 3.65982344e+01],
       [2.21406416e+02, 1.33943076e+03, 8.10308393e+03]])

1
2
3

# _ 表示上（最近）一个输出
# logspace 结果 log 后就是上面 linspace 的结果
np.log(_)

array([[0. , 1.8, 3.6],
       [5.4, 7.2, 9. ]])

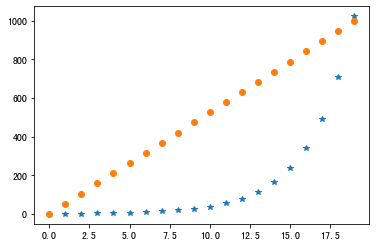
下面我们更进一步看一下：

N = 20
x = np.arange(N)
y1 = np.linspace(0, 10, N) * 100
y2 = np.logspace(0, 10, N, base=2)

plt.plot(x, y2, '*');
plt.plot(x, y1, 'o');

png

1
2
3

# 检查每个元素是否为 True
# base 的 指数为 linspace 得到的就是 logspace
np.alltrue(2 ** np.linspace(0, 10, N)  == y2)

True

⚠️ 补充：关于 array 的条件判断

# 不能直接用 if 判断 array 是否符合某个条件
arr = np.array([1, 2, 3])
cond1 = arr > 2
cond1

array([False, False,  True])

1 2	if cond1: print("这不行")

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-184-6bd8dc445309> in <module>
----> 1 if cond1:
      2     print("这不行")


ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

# 即便你全是 True 它也不行
arr = np.array([1, 2, 3])
cond2 = arr > 0
cond2

array([ True,  True,  True])

1 2	if cond2: print("这还不行")

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-187-7fedc8ba71a0> in <module>
----> 1 if cond2:
      2     print("这还不行")


ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

1
2
3

# 咱们只能用 any 或 all，这个很容易犯错，请务必注意。
if cond1.any():
    print("只要有一个为True就可以，所以——我可以")

只要有一个为True就可以，所以——我可以

1 2	if cond2.all(): print("所有值为True才可以，我正好这样")

所有值为True才可以，我正好这样

使用 ones/zeros 创建

⭐

创建全 1/0 array 的快捷方式。需要注意的是 np.zeros_like 或 np.ones_like，二者可以快速生成给定 array 一样 shape 的 0 或 1 向量，这在需要 Mask 某些位置时可能会用到。

⚠️ 需要注意的是：创建出来的 array 默认是 float 类型。

1	np.ones(3)

array([1., 1., 1.])

1	np.ones((2, 3))

array([[1., 1., 1.],
       [1., 1., 1.]])

1	np.zeros((2,3,4))

array([[[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]],

       [[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]]])

1 2	# 像给定向量那样的 0 向量（ones_like 是 1 向量） np.zeros_like(np.ones((2,3,3)))

array([[[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]]])

使用 random 生成

⭐⭐⭐⭐⭐

如果要在这一节选一个最重要的 API，那一定是 random 无疑了，这里我们只介绍几个比较常用的「生产」数据相关的 API。它们经常用于随机生成训练或测试数据，神经网路初始化等。

⚠️ 需要注意的是：这里我们统一推荐使用新的 API 方式创建，即通过 np.random.default_rng() 先生成 Generator，然后再在此基础上生成各种分布的数据（记忆更加简便清晰）。不过我们依然会介绍就的 API 用法，因为很多代码中使用的还是旧的，您可以混个眼熟。

1 2	# 0-1 连续均匀分布 np.random.rand(2, 3)

array([[0.42508994, 0.5842191 , 0.09248675],
       [0.656858  , 0.88171822, 0.81744539]])

1 2	# 单个数 np.random.rand()

0.29322641374172986

1 2	# 0-1 连续均匀分布 np.random.random((3, 2))

array([[0.17586271, 0.5061715 ],
       [0.14594537, 0.34365713],
       [0.28714656, 0.40508807]])

1 2	# 指定上下界的连续均匀分布 np.random.uniform(-1, 1, (2, 3))

array([[ 0.66638982, -0.65327069, -0.21787878],
       [-0.63552782,  0.51072282, -0.14968825]])

# 上面两个的区别是 shape 的输入方式不同，无伤大雅了
# 不过从 1.17 版本后推荐这样使用（以后大家可以用新的方法）
# rng 是个 Generator，可用于生成各种分布
rng = np.random.default_rng(42)
rng

Generator(PCG64) at 0x111B5C5E0

1 2	# 推荐的连续均匀分布用法 rng.random((2, 3))

array([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235]])

1 2	# 可以指定上下界，所以更加推荐这种用法 rng.uniform(0, 1, (2, 3))

array([[0.47673156, 0.59702442, 0.63523558],
       [0.68631534, 0.77560864, 0.05803685]])

1 2	# 随机整数（离散均匀分布），不超过给定的值（10） np.random.randint(10, size=2)

array([6, 3])

1 2	# 随机整数（离散均匀分布），指定上下界和 shape np.random.randint(0, 10, (2, 3))

array([[8, 6, 1],
       [3, 8, 1]])

1 2	# 上面推荐的方法，指定大小和上界 rng.integers(10, size=2)

array([9, 7])

1 2	# 上面推荐的方法，指定上下界 rng.integers(0, 10, (2, 3))

array([[5, 9, 1],
       [8, 5, 7]])

1 2	# 标准正态分布 np.random.randn(2, 4)

array([[-0.61241167, -0.55218849, -0.50470617, -1.35613877],
       [-1.34665975, -0.74064846, -2.5181665 ,  0.66866357]])

1 2	# 上面推荐的标准正态分布用法 rng.standard_normal((2, 4))

array([[ 0.09130331,  1.06124845, -0.79376776, -0.7004211 ],
       [ 0.71545457,  1.24926923, -1.22117522,  1.23336317]])

1 2	# 高斯分布 np.random.normal(0, 1, (3, 5))

array([[ 0.30037773, -0.17462372,  0.23898533,  1.23235421,  0.90514996],
       [ 0.90269753, -0.5679421 ,  0.8769029 ,  0.81726869, -0.59442623],
       [ 0.31453468, -0.18190156, -2.95932929, -0.07164822, -0.23622439]])

1 2	# 上面推荐的高斯分布用法 rng.normal(0, 1, (3, 5))

array([[ 2.20602146, -2.17590933,  0.80605092, -1.75363919,  0.08712213],
       [ 0.33164095,  0.33921626,  0.45251278, -0.03281331, -0.74066207],
       [-0.61835785, -0.56459129,  0.37724436, -0.81295739,  0.12044035]])

总之，一般会用的就是2个分布：均匀分布和正态（高斯）分布。另外，size 可以指定 shape。

1	rng = np.random.default_rng(42)

1 2	# 离散均匀分布 rng.integers(low=0, high=10, size=5)

array([0, 7, 6, 4, 4])

1 2	# 连续均匀分布 rng.uniform(low=0, high=10, size=5)

array([6.97368029, 0.94177348, 9.75622352, 7.61139702, 7.86064305])

1 2	# 正态（高斯）分布 rng.normal(loc=0.0, scale=1.0, size=(2, 3))

array([[-0.01680116, -0.85304393,  0.87939797],
       [ 0.77779194,  0.0660307 ,  1.12724121]])

从文件读取

⭐

这小节主要用于加载实现存储好的权重参数或预处理好的数据集，有时候会比较方便，比如训练好的模型参数加载到内存里用来提供推理服务，或者耗时很久的预处理数据直接存起来，多次实验时不需要重新处理。

⚠️ 需要注意的是：存储时不需要写文件名后缀，会自动添加。

1 2	# 直接将给定矩阵存为 a.npy np.save('./data/a', np.array([[1, 2, 3], [4, 5, 6]]))

1 2	# 可以将多个矩阵存在一起，名为 `b.npz` np.savez("./data/b", a=np.arange(12).reshape(3, 4), b=np.arange(12.).reshape(4, 3))

1 2	# 和上一个一样，只是压缩了 np.savez_compressed("./data/c", a=np.arange(12).reshape(3, 4), b=np.arange(12.).reshape(4, 3))

1 2	# 加载单个 array np.load("data/a.npy")

array([[1, 2, 3],
       [4, 5, 6]])

1 2	# 加载多个，可以像字典那样取出对应的 array arr = np.load("data/b.npz")

arr["a"]

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

arr["b"]

array([[ 0.,  1.,  2.],
       [ 3.,  4.,  5.],
       [ 6.,  7.,  8.],
       [ 9., 10., 11.]])

1 2	# 后缀都一样，你干脆当它和上面的没区别即可 arr = np.load("data/c.npz")

arr["b"]

array([[ 0.,  1.,  2.],
       [ 3.,  4.,  5.],
       [ 6.,  7.,  8.],
       [ 9., 10., 11.]])

统计和属性

本节我们从 array 的基本统计属性入手，对刚刚创建的 array 进一步的了解。主要包括以下几个方面：

尺寸相关
最大、最小、中位、分位值
平均、求和、标准差等

都是描述性统计相关的指标，对于我们从整体了解一个 array 很有帮助。其中，用到最多的是尺寸相关的「shape」，最大、最小值，平均值、求和等。

本节的内容非常简单，您只需要特别关注（记住）两个重要的特性：

按维度（指定 axis）求结果。一般0表示列1表示行，可以用「沿着行/列操作」这样理解，不确定时可以拿个例子试一下。
计算后保持维度（keepdims=True）

另外，为了便于操作，我们使用一个随机生成的 array 作为操作对象；同时，我们指定了 seed，这样每次运行，每个人看到的结果都是一样的。一般我们在训练模型时，往往需要指定 seed，这样才能在「同等条件」下进行调参。

#  先创建一个 Generator
rng = np.random.default_rng(seed=42)
#  再生成一个均匀分布
arr = rng.uniform(0, 1, (3, 4))
arr

array([[0.77395605, 0.43887844, 0.85859792, 0.69736803],
       [0.09417735, 0.97562235, 0.7611397 , 0.78606431],
       [0.12811363, 0.45038594, 0.37079802, 0.92676499]])

尺寸相关

⭐⭐

这一小节主要包括：维度、形状和数据量，其中形状 shape 我们用到的最多。

⚠️ 需要注意的是：size 不是 shape，ndim 表示有几个维度。

1 2	# 维度，array 是二维的（两个维度） arr.ndim

`np.shape`

1 2	# 形状，返回一个 Tuple arr.shape

(3, 4)

1 2	# 数据量 arr.size

最值分位

⭐⭐⭐

这一小节主要包括：最大值、最小值、中位数、其他分位数，其中『最大值和最小值』我们平时用到的最多。

⚠️ 需要注意的是：分位数可以是 0-1 的任意小数（表示对应分位），而且分位数并不一定在原始的 array 中。

arr

array([[0.77395605, 0.43887844, 0.85859792, 0.69736803],
       [0.09417735, 0.97562235, 0.7611397 , 0.78606431],
       [0.12811363, 0.45038594, 0.37079802, 0.92676499]])

1 2	# 所有元素中最大的 arr.max()

0.9756223516367559

`np.max/min`

1 2	# 按维度（列）最大值 arr.max(axis=0)

array([0.77395605, 0.97562235, 0.85859792, 0.92676499])

1 2	# 同理，按行 arr.max(axis=1)

array([0.85859792, 0.97562235, 0.92676499])

# 是否保持原来的维度
# 这个需要特别注意下，很多深度学习模型中都需要保持原有的维度进行后续计算
# shape 是 (3,1)，array 的 shape 是 (3,4)，按行，同时保持了行的维度
arr.min(axis=1, keepdims=True)

array([[0.43887844],
       [0.09417735],
       [0.12811363]])

1 2	# 保持维度：（1，4），原始array是（3，4） arr.min(axis=0, keepdims=True)

array([[0.09417735, 0.43887844, 0.37079802, 0.69736803]])

1 2	# 一维了 arr.min(axis=0, keepdims=False)

array([0.09417735, 0.43887844, 0.37079802, 0.69736803])

1 2	# 另一种用法，不过我们一般习惯使用上面的用法，其实两者一回事 np.amax(arr, axis=0)

array([0.77395605, 0.97562235, 0.85859792, 0.92676499])

1 2	# 同 amax np.amin(arr, axis=1)

array([0.43887844, 0.09417735, 0.12811363])

1
2
3

# 中位数
# 其他用法和 max，min 是一样的
np.median(arr)

0.7292538655248584

1 2	# 分位数，按列取1/4数 np.quantile(arr, q=0.25, axis=0)

array([0.11114549, 0.44463219, 0.56596886, 0.74171617])

1 2	# 分位数，按行取 3/4，同时保持维度 np.quantile(arr, q=0.75, axis=1, keepdims=True)

array([[0.79511652],
       [0.83345382],
       [0.5694807 ]])

1
2
3

# 分位数，注意，分位数可以是 0-1 之间的任何数字（分位）
# 如果是 1/2 分位，那正好是中位数
np.quantile(arr, q=1/2, axis=1)

array([0.73566204, 0.773602  , 0.41059198])

平均求和标准差

⭐⭐⭐

这一小节主要包括：平均值、累计求和、方差、标准差等进一步的统计指标。其中使用最多的是「平均值」。

arr

array([[0.77395605, 0.43887844, 0.85859792, 0.69736803],
       [0.09417735, 0.97562235, 0.7611397 , 0.78606431],
       [0.12811363, 0.45038594, 0.37079802, 0.92676499]])

`np.average`

1 2	# 平均值 np.average(arr)

0.6051555606435642

1 2	# 按维度平均（列） np.average(arr, axis=0)

array([0.33208234, 0.62162891, 0.66351188, 0.80339911])

# 另一个计算平均值的 API
# 它与 average 的主要区别是，np.average 可以指定权重，即可以用于计算加权平均
# 一般建议使用 average，忘掉 mean 吧！
np.mean(arr, axis=0)

array([0.33208234, 0.62162891, 0.66351188, 0.80339911])

`np.sum`

1 2	# 求和，不多说了，类似 np.sum(arr, axis=1)

array([2.76880044, 2.61700371, 1.87606258])

1	np.sum(arr, axis=1, keepdims=True)

array([[2.76880044],
       [2.61700371],
       [1.87606258]])

1 2	# 按列累计求和 np.cumsum(arr, axis=0)

array([[0.77395605, 0.43887844, 0.85859792, 0.69736803],
       [0.8681334 , 1.41450079, 1.61973762, 1.48343233],
       [0.99624703, 1.86488673, 1.99053565, 2.41019732]])

1 2	# 按行累计求和 np.cumsum(arr, axis=1)

array([[0.77395605, 1.21283449, 2.07143241, 2.76880044],
       [0.09417735, 1.0697997 , 1.8309394 , 2.61700371],
       [0.12811363, 0.57849957, 0.94929759, 1.87606258]])

1 2	# 标准差，用法类似 np.std(arr)

0.28783096517727075

1 2	# 按列求标准差 np.std(arr, axis=0)

array([0.3127589 , 0.25035525, 0.21076935, 0.09444968])

1 2	# 方差 np.var(arr, axis=1)

array([0.02464271, 0.1114405 , 0.0839356 ])

形状和转换

array 大多数情况下都是以多维的形式出现的，一般对超过二维的多维 array 称为「张量」，二维矩阵，一维向量。因为多维度，所以自然而然地涉及到形状的改变和转换，可以算是张量最基础的「操作」了。

本节我们主要涉及以下三个方面：

改变形状
反序
转置

其中，改变形状和转置都非常常用，我们建议您熟练掌握。

改变形状

⭐⭐⭐⭐⭐

这小节里面的 API 使用非常高频，尤其是扩展 1 维度的 expand_dims 和去除 1 维度的 squeeze，您未来会在很多神经网络架构中看到这俩货的身影。

⚠️ 需要注意的是：无论是扩展还是缩减，多或少的 shape 都是 1，squeeze 时如果指定维度，则该维度 shape 必须是 1。

# 换个整数的随机 array
rng = np.random.default_rng(seed=42)
arr = rng.integers(1, 100, (3, 4))
arr

array([[ 9, 77, 65, 44],
       [43, 86,  9, 70],
       [20, 10, 53, 97]])

1 2	# 有时候您可能需要将多维 array 打平 arr.ravel()

array([ 9, 77, 65, 44, 43, 86,  9, 70, 20, 10, 53, 97])

arr.shape

(3, 4)

`np.expand_dims`

1
2
3

#### 扩展 1 个维度，需要（必须）指定维度
# 其实就是多嵌套了一下
np.expand_dims(arr, 1).shape

(3, 1, 4)

1
2
3

# 扩充维度
expanded = np.expand_dims(arr, axis=(1, 3, 4))
expanded.shape

(3, 1, 4, 1, 1)

1 2	# 扩充维度不能跳跃 expanded = np.expand_dims(arr, axis=(1, 3, 8))

---------------------------------------------------------------------------

AxisError                                 Traceback (most recent call last)

<ipython-input-344-2c2510eb807f> in <module>
      1 # 扩充维度不能跳跃
----> 2 expanded = np.expand_dims(arr, axis=(1, 3, 8))


<__array_function__ internals> in expand_dims(*args, **kwargs)


/usr/local/lib/python3.8/site-packages/numpy/lib/shape_base.py in expand_dims(a, axis)
    595 
    596     out_ndim = len(axis) + a.ndim
--> 597     axis = normalize_axis_tuple(axis, out_ndim)
    598 
    599     shape_it = iter(a.shape)


/usr/local/lib/python3.8/site-packages/numpy/core/numeric.py in normalize_axis_tuple(axis, ndim, argname, allow_duplicate)
   1356             pass
   1357     # Going via an iterator directly is slower than via list comprehension.
-> 1358     axis = tuple([normalize_axis_index(ax, ndim, argname) for ax in axis])
   1359     if not allow_duplicate and len(set(axis)) != len(axis):
   1360         if argname:


/usr/local/lib/python3.8/site-packages/numpy/core/numeric.py in <listcomp>(.0)
   1356             pass
   1357     # Going via an iterator directly is slower than via list comprehension.
-> 1358     axis = tuple([normalize_axis_index(ax, ndim, argname) for ax in axis])
   1359     if not allow_duplicate and len(set(axis)) != len(axis):
   1360         if argname:


AxisError: axis 8 is out of bounds for array of dimension 5

`np.squeeze`

1 2	# squeeze 指定 axis 的shape必须为1 np.squeeze(expanded, axis=0)

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-345-8a712eef1189> in <module>
      1 # squeeze 指定 axis 的shape必须为1
----> 2 np.squeeze(expanded, axis=0)


<__array_function__ internals> in squeeze(*args, **kwargs)


/usr/local/lib/python3.8/site-packages/numpy/core/fromnumeric.py in squeeze(a, axis)
   1493         return squeeze()
   1494     else:
-> 1495         return squeeze(axis=axis)
   1496 
   1497 


ValueError: cannot select an axis to squeeze out which has size not equal to one

1 2	# 如果指定了维度，那就只会去除该维度，指定的维度必须为 1 np.squeeze(expanded, axis=1).shape

(3, 3, 1, 1)

1 2	# 去除所有维度为 1 的 np.squeeze(expanded).shape

(3, 3)

`np.reshape/arr.reshape`

1
2
3

# reshape 成另一个形状
# 也可以直接变为一维向量
arr.reshape(2, 2, 3)

array([[[ 9, 77, 65],
        [44, 43, 86]],

       [[ 9, 70, 20],
        [10, 53, 97]]])

1
2
3

# 可以偷懒，使用 -1 表示其他维度（此处 -1 为 3），注意，reshape 参数可以是 tuple 或连续整数
arr1 = arr.reshape((4, -1))
arr1

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

1 2	# 元素数量必须与原array一致 arr.reshape(3, 3)

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-348-67f1d69569ea> in <module>
      1 # 元素数量必须与原array一致
----> 2 arr.reshape(3, 3)


ValueError: cannot reshape array of size 12 into shape (3,3)

# 另一种变换形状的方式 —— 原地变换
# 不过不能用-1
# 另外 resize 不一定和原来的元素数量一样多
arr2 = arr.resize((4, 3))
# 注意：上面的 reshape 会生成一个新的 array，但 resize 不会，所以我们需要用原变量名将它显示出来
# arr2 没有值
arr2

arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

1 2	# 直接 resize，如果元素数量多时会提示错误 arr.resize((2, 3))

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-351-a23c63ab1d76> in <module>
      1 # 直接 resize，如果元素数量多时会提示错误
----> 2 arr.resize((2, 3))


ValueError: cannot resize an array that references or is referenced
by another array in this way.
Use the np.resize function or refcheck=False

# 可以copy一份
arrcopy = np.copy(arr)
arrcopy.resize((2, 3))
arrcopy

array([[ 9, 77, 65],
       [44, 43, 86]])

1 2	# arr 保持不变 arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

# 也可以将 refcheck 设为 False
# 此时 arr 会发生变化
# 元素数量超出时，截断；元素数量不够时，0填充
arr.resize((2,3), refcheck=False)
arr

array([[ 9, 77, 65],
       [44, 43, 86]])

1 2	arr.resize((3, 3), refcheck=False) arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 0,  0,  0]])

arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 0,  0,  0]])

1
2
3

# 如果用 np.resize 会略有不同
# 元素数量不够时，会自动复制
np.resize(arr, (5, 3))

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 0,  0,  0],
       [ 9, 77, 65],
       [44, 43, 86]])

1 2	# 元素数量多出来时，会自动截断 np.resize(arr, (2, 2))

array([[ 9, 77],
       [65, 44]])

反序

⭐

也可以看作是一种对原数组的转换，用的不多，可以了解一下，为接下来的索引和切片做个热身。

如果给一个字符串或数组让您反序，您可能会想到很多种方法，比如：reversed，或者写一个方法，或者用 Python list 的索引功能，而这也是 numpy 中 array 反序的方式。

1
2
3

# 字符串
s = "uevol"
s[::-1]

'loveu'

1
2
3

# 数组
lst = [1, "1", 5.2]
lst[::-1]

[5.2, '1', 1]

arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

1 2	# 我们按上面的套路：默认列反序 arr[::-1]

array([[10, 53, 97],
       [ 9, 70, 20],
       [44, 43, 86],
       [ 9, 77, 65]])

1 2	# 列不变行反序 arr[::-1, :]

array([[10, 53, 97],
       [ 9, 70, 20],
       [44, 43, 86],
       [ 9, 77, 65]])

1 2	# 在不同维度上操作：行不变列反序 arr[:, ::-1]

array([[65, 77,  9],
       [86, 43, 44],
       [20, 70,  9],
       [97, 53, 10]])

1 2	# 行变列也变 arr[::-1, ::-1]

array([[97, 53, 10],
       [20, 70,  9],
       [86, 43, 44],
       [65, 77,  9]])

转置

⭐⭐⭐

转置是线性代数的基本操作，拿二维矩阵为例，通俗理解就是把它放倒，shape 反转，行变成列，列成为行。当然，对于多维也是类似的。我们建议您二维矩阵用 arr.T（会快很多），超过二维的张量可以用 np.transpose，会更加灵活些。

⚠️ 需要注意的是：一维数组转置还是自己。

1 2	# 一维 np.array([1,2]).T.shape

(2,)

arr

array([[ 9, 77, 65],
       [44, 43, 86],
       [ 9, 70, 20],
       [10, 53, 97]])

`arr.T`

1 2	# 简便用法，把所有维度顺序都给倒过来 arr.T

array([[ 9, 44,  9, 10],
       [77, 43, 70, 53],
       [65, 86, 20, 97]])

1 2	# 将 shape=(1,1,3,4) 的转置后得到 shape=(4,3,1,1) arr.reshape(1, 1, 3, 4).T.shape

(4, 3, 1, 1)

1 2	# 同上 arr.reshape(1, 2, 2, 1, 3, 1).T.shape

(1, 3, 1, 2, 2, 1)

`np.transpose`

1 2	# 这种转置方式可以指定 axes np.transpose(arr)

array([[ 9, 44,  9, 10],
       [77, 43, 70, 53],
       [65, 86, 20, 97]])

1 2	# 不指定 axes 时和 .T 是一样的 np.transpose(arr.reshape(1, 2, 2, 1, 3, 1)).shape

(1, 3, 1, 2, 2, 1)

# 指定 axes，不过 axes 数量必须包含所有维度的序列
# 比如两个维度就是 (0, 1)，四个就是 (0, 1, 2, 3)
# 当然，顺序可以改变，比如下面就是只转置第 2 个和第 3 个维度
# 注意，只有超过 2 维时，这样才有意义
# 下面的结果中，中间2个维度被调换顺序了，顺序就在axes中指定的
np.transpose(arr.reshape(1, 1, 3, 4), axes=(0, 2, 1, 3)).shape

(1, 3, 1, 4)

分解和组合

这节我们主要学习 array 的分解和组合，本节是所有章节中最重要的一节，通过本节内容，您可以充分了解 numpy（以及 Python 语言）的强大，这种操作上的优雅不能说后无来者，但至少前无古人了。

内容大致包括以下小节：

切片和索引
拼接
重复
分拆

其中，重中之重是「切片和索引」，它基础、它高频、它无处不在。我们强烈建议您熟练掌握，其他三个相对简单，只需要各记住一个 API 即可。

切片和索引

⭐⭐⭐⭐⭐

划重点！切片和索引是通过对已有 array 进行操作而得到想要的「部分」元素的行为过程。其核心动作可以概括为：按维度根据 start:stop:step 操作 array。

这部分内容的核心是把处理按维度分开，不处理的维度统一用 : 或 ... 代替；在看操作时，也要首先关注「,」在哪里。要处理的维度和之前 arange linspace 等接口使用方法是一样的。

⚠️ 需要注意的是：引支持负数，即从后往前索引。

1
2
3

rng = np.random.default_rng(42)
arr = rng.integers(0, 20, (5, 4))
arr

array([[ 1, 15, 13,  8],
       [ 8, 17,  1, 13],
       [ 4,  1, 10, 19],
       [14, 15, 14, 15],
       [10,  2, 16,  9]])

`index/slice`

1 2	# 最简单的索引，取第 0 行 arr[0]

array([ 1, 15, 13,  8])

1 2	# 最简单的切片，取第 0 行第 1 个元素 arr[0, 1]

1 2	# 然后带点范围第 1-2 行 arr[0:3]

array([[ 1, 15, 13,  8],
       [ 8, 17,  1, 13],
       [ 4,  1, 10, 19]])

1 2	# 离散也可以：第 1，3 行 arr[[0, 3]]

array([[ 1, 15, 13,  8],
       [14, 15, 14, 15]])

arr

array([[ 1, 15, 13,  8],
       [ 8, 17,  1, 13],
       [ 4,  1, 10, 19],
       [14, 15, 14, 15],
       [10,  2, 16,  9]])

1 2	# 再来加上维度：第 1-2 行，第 1 列 arr[1:3, 1]

array([17,  1])

1 2	# 离散也是一样：第 1，3 行，第 0 列 arr[[1,3], [0]]

array([ 8, 14])

1 2	# 还可以有简写：到最后或到开始。如第 3 行到最后一行 arr[3:]

array([[14, 15, 14, 15],
       [10,  2, 16,  9]])

1 2	# 开始到第 3 行，第 1-3 列 arr[:3, 1:3]

array([[15, 13],
       [17,  1],
       [ 1, 10]])

1 2	# 还可以来点跳跃，步长：start:stop:step，第 1 行到第 4 行，间隔为 2，即第 1、3 行 arr[1: 4: 2]

array([[ 8, 17,  1, 13],
       [14, 15, 14, 15]])

1 2	# 加上列也可以哦，第 1、3 行，第 0、2 列 arr[1:4:2, 0:3:2]

array([[ 8,  1],
       [14, 14]])

arr

array([[ 1, 15, 13,  8],
       [ 8, 17,  1, 13],
       [ 4,  1, 10, 19],
       [14, 15, 14, 15],
       [10,  2, 16,  9]])

1 2	# 第一列的值，其实是所有其他维度第 1 维的值 arr[...,1]

array([15, 17,  1, 15,  2])

1 2	# 与上面类似，但用的更多 arr[:,1]

array([15, 17,  1, 15,  2])

拼接

⭐⭐⭐⭐

有时候我们需要对已有的几个 array 进行拼接以形成一个大的 array（常见的例子比如不同类型特征的拼接）。本小节严格来说只有两个 API：np.concatenate 和 np.stack，前者是拼接，后者是堆叠（会增加一个维度），都可以指定维度。记住，有它俩就够了。

⚠️ 需要注意的是：hstack 和 vstack 和 stack 没关系，反而是 concatenate。

rng = np.random.default_rng(42)

arr1 = rng.random((2, 3))
arr2 = rng.random((2, 3))
arr1, arr2

(array([[0.77395605, 0.43887844, 0.85859792],
        [0.69736803, 0.09417735, 0.97562235]]),
 array([[0.7611397 , 0.78606431, 0.12811363],
        [0.45038594, 0.37079802, 0.92676499]]))

`np.concatenate`

1 2	# 默认沿axis=0（列）连接 np.concatenate((arr1, arr2))

array([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235],
       [0.7611397 , 0.78606431, 0.12811363],
       [0.45038594, 0.37079802, 0.92676499]])

1 2	# 沿 axis=1（行）连接 np.concatenate((arr1, arr2), axis=1)

array([[0.77395605, 0.43887844, 0.85859792, 0.7611397 , 0.78606431,
        0.12811363],
       [0.69736803, 0.09417735, 0.97562235, 0.45038594, 0.37079802,
        0.92676499]])

1
2
3

# 竖直按行顺序拼接
# 注意：vstack 虽然看起来是 stack，但其实它是 concatenate，建议您只使用 `np.concatenate`
np.vstack((arr1, arr2))

array([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235],
       [0.7611397 , 0.78606431, 0.12811363],
       [0.45038594, 0.37079802, 0.92676499]])

1
2
3

# 水平按列顺序拼接
# 道理和 vstack 一样，建议使用 `np.concatenate` axis=1
np.hstack((arr1, arr2))

array([[0.77395605, 0.43887844, 0.85859792, 0.7611397 , 0.78606431,
        0.12811363],
       [0.69736803, 0.09417735, 0.97562235, 0.45038594, 0.37079802,
        0.92676499]])

`np.stack`

1 2	# 堆叠，默认根据 axis=0 进行 np.stack((arr1, arr2))

array([[[0.77395605, 0.43887844, 0.85859792],
        [0.69736803, 0.09417735, 0.97562235]],

       [[0.7611397 , 0.78606431, 0.12811363],
        [0.45038594, 0.37079802, 0.92676499]]])

_.shape

(2, 2, 3)

1 2	# 堆叠，根据 axis=2 np.stack((arr1, arr2), axis=2)

array([[[0.77395605, 0.7611397 ],
        [0.43887844, 0.78606431],
        [0.85859792, 0.12811363]],

       [[0.69736803, 0.45038594],
        [0.09417735, 0.37079802],
        [0.97562235, 0.92676499]]])

1 2	# _ 表示上一个 Cell 的输出结果 _.shape

(2, 3, 2)

1 2	# 纵深按 axis=2 堆叠，不管它就行，我们认准 `stack` np.dstack((arr1, arr2))

array([[[0.77395605, 0.7611397 ],
        [0.43887844, 0.78606431],
        [0.85859792, 0.12811363]],

       [[0.69736803, 0.45038594],
        [0.09417735, 0.37079802],
        [0.97562235, 0.92676499]]])

_.shape

(2, 3, 2)

重复

⭐⭐⭐

重复其实是另一种拼接方式，它也可以指定要重复的维度。在有些深度学习模型数据构建中非常有用（方便）。

⚠️ 需要注意的是：是一个维度一个维度依次重复，而不是整个 array 重复。

1
2
3

rng = np.random.default_rng(42)
arr = rng.integers(0, 10, (3, 4))
arr

array([[0, 7, 6, 4],
       [4, 8, 0, 6],
       [2, 0, 5, 9]])

1 2	# 在 axis=0（沿着列）上重复 2 次 np.repeat(arr, 2, axis=0)

array([[0, 7, 6, 4],
       [0, 7, 6, 4],
       [4, 8, 0, 6],
       [4, 8, 0, 6],
       [2, 0, 5, 9],
       [2, 0, 5, 9]])

1 2	# 在 axis=1（沿着行）上重复 3 次 np.repeat(arr, 3, axis=1)

array([[0, 0, 0, 7, 7, 7, 6, 6, 6, 4, 4, 4],
       [4, 4, 4, 8, 8, 8, 0, 0, 0, 6, 6, 6],
       [2, 2, 2, 0, 0, 0, 5, 5, 5, 9, 9, 9]])

分拆

⭐⭐⭐

有拼接堆叠自然就有拆分，注意这不是切片和索引，就是将 array 拆成想要的几份。用的不是特别多，API 只要记住 np.split 就行了，其他的都是快捷方式。

⚠️ 需要注意的是：分拆的 axis 是对该维度进行拆分。

1
2
3

rng = np.random.default_rng(42)
arr = rng.integers(1, 100, (6, 4))
arr

array([[ 9, 77, 65, 44],
       [43, 86,  9, 70],
       [20, 10, 53, 97],
       [73, 76, 72, 78],
       [51, 13, 84, 45],
       [50, 37, 19, 92]])

`np.split`

1 2	# 默认切分列（axis=0），切成 3 份 np.split(arr, 3)

[array([[ 9, 77, 65, 44],
        [43, 86,  9, 70]]),
 array([[20, 10, 53, 97],
        [73, 76, 72, 78]]),
 array([[51, 13, 84, 45],
        [50, 37, 19, 92]])]

1 2	# （axis=1）切分行 np.split(arr, 2, axis=1)

[array([[ 9, 77],
        [43, 86],
        [20, 10],
        [73, 76],
        [51, 13],
        [50, 37]]),
 array([[65, 44],
        [ 9, 70],
        [53, 97],
        [72, 78],
        [84, 45],
        [19, 92]])]

1 2	# 和上面的一个效果 np.vsplit(arr, 3)

[array([[ 9, 77, 65, 44],
        [43, 86,  9, 70]]),
 array([[20, 10, 53, 97],
        [73, 76, 72, 78]]),
 array([[51, 13, 84, 45],
        [50, 37, 19, 92]])]

1 2	# 等价的用法 np.hsplit(arr, 2)

[array([[ 9, 77],
        [43, 86],
        [20, 10],
        [73, 76],
        [51, 13],
        [50, 37]]),
 array([[65, 44],
        [ 9, 70],
        [53, 97],
        [72, 78],
        [84, 45],
        [19, 92]])]

筛选和过滤

这小节与索引和切片有点类似，但倾向于从「整体」中统一筛选出「符合条件」的内容，而索引和切片更多的是依照「某种方法」切出一块内容。本小节内容同样非常重要，可以算第二个最重要的小节。主要包括以下内容：

条件筛选
提取（按条件）
抽样（按分布）
最大最小 index（特殊值）

这几个内容都很重要，使用的也非常高频。条件筛选经常用于 Mask 或异常值处理，提取则常用于结果过滤，抽样常用在数据生成（比如负样本抽样），最大最小 index 则常见于机器学习模型预测结果判定中（根据最大概率所在的 index 决定结果属于哪一类）。

1
2
3

rng = np.random.default_rng(42)
arr = rng.integers(1, 100, (3, 4))
arr

array([[ 9, 77, 65, 44],
       [43, 86,  9, 70],
       [20, 10, 53, 97]])

条件筛选

⭐⭐⭐

顾名思义，根据一定的条件对 array 进行筛选（标记）并后续处理。核心 API 是 np.where。

⚠️ 需要注意的是：where 分别返回各维度的 index，赋值的是「不满足」条件的。

1 2	# 条件筛选，可以直接在整个 array 上使用条件 arr > 50

array([[False,  True,  True, False],
       [False,  True, False,  True],
       [False, False,  True,  True]])

1 2	# 返回满足条件的索引，因为是两个维度，所以会返回两组结果 np.where(arr > 50)

(array([0, 0, 1, 1, 2, 2]), array([1, 2, 1, 3, 2, 3]))

1 2	# 不满足条件的赋值，将 <=50 的替换为 -1 np.where(arr > 50, arr, -1)

array([[-1, 77, 65, -1],
       [-1, 86, -1, 70],
       [-1, -1, 53, 97]])

提取

⭐

在 array 中提取指定条件的值。

⚠️ 需要注意的是：提取和唯一值返回的都是一维向量。

1 2	# 提取指定条件的值 np.extract(arr > 50, arr)

array([77, 65, 86, 70, 53, 97])

1 2	# 唯一值，是另一种形式的提取 np.unique(arr)

array([ 9, 10, 20, 43, 44, 53, 65, 70, 77, 86, 97])

抽样

⭐⭐⭐⭐⭐

我们在跑模型时常常需要使用部分数据对整个过程快速验证，您当然可以使用 np.random 生成模拟数据。但有真实数据时，从真实数据中随机抽样会比较好。

⚠️ 需要注意的是：抽样的集合要求为一维向量（一般是数据的 index）。

rng = np.random.default_rng(42)
# 第一个参数是要抽样的集合，如果是一个整数，则表示从 0 到该值
# 第二个参数是样本大小
# 第三个参数表示结果是否可以重复
# 第四个参数表示出现的概率，长度和第一个参数一样

# 由于（0 1 2 3）中 2 和 3 的概率比较高，自然就选择了 2 和 3
rng.choice(4, 2, replace=False, p=[0.1, 0.2, 0.3, 0.4])

array([3, 2])

# 旧的 API
# 如果是抽样语料的 index，更多的方法是这样：
data_size = 10000
np.random.choice(data_size, 50, replace=False)

array([6339, 4894, 1531, 7814,  224, 9538, 9619, 3801, 3359, 3617, 2795,
       6627, 8501, 1681, 4212, 5085, 2439,  744, 9123, 6733, 5688, 5480,
       6983, 7058,  310, 1838, 5072,  746, 5873, 9372, 5953, 4944, 1780,
        464, 1247,  845, 1807, 7354, 4925,  547, 2996, 3909, 7344, 9617,
       8642,  661, 2453, 5475,  228, 2427])

最值 Index

⭐⭐⭐⭐⭐

这小节主要是两个 API：np.argmax(min) 和 np.argsort，当然最常用的还是第一个，不用说，自然是可以（需要）指定 axis 的。

1
2
3

rng = np.random.default_rng(42)
arr = rng.uniform(1, 100, (3, 4))
arr

array([[77.62164881, 44.44896554, 86.00119407, 70.03943488],
       [10.32355744, 97.58661281, 76.3528305 , 78.82036622],
       [13.68324963, 45.58820785, 37.7090044 , 92.7497339 ]])

`np.argmax/argmin`

1 2	# 所有值中最大值的 Index，基本不这么用 np.argmax(arr)

1 2	# 按列（axis=0）最大值的 Index np.argmax(arr, axis=0)

array([0, 1, 0, 2])

1 2	# 按行（axis=1）最小值的 Index np.argmin(arr, axis=1)

array([1, 0, 0])

`np.argsort`

arr

array([[77.62164881, 44.44896554, 86.00119407, 70.03943488],
       [10.32355744, 97.58661281, 76.3528305 , 78.82036622],
       [13.68324963, 45.58820785, 37.7090044 , 92.7497339 ]])

1 2	# 默认按行（axis=1）排序的索引 np.argsort(arr)

array([[1, 3, 0, 2],
       [0, 2, 3, 1],
       [0, 2, 1, 3]])

1 2	# 数据按行（axis=1）排序的索引，同上 np.argsort(arr, axis=1)

array([[1, 3, 0, 2],
       [0, 2, 3, 1],
       [0, 2, 1, 3]])

1 2	# 数据按列（axis=0）排序索引 np.argsort(arr, axis=0)

array([[1, 0, 2, 0],
       [2, 2, 1, 1],
       [0, 1, 0, 2]])

矩阵和运算

这一节我们将聚焦矩阵和相关的运算，主要包括：

算术（四则运算及其他基础算术）
广播
矩阵相关

这些内容其实使用非常普遍，普遍到我们甚至都不会察觉到自己在使用，而且也非常简单。当然，高纬度的计算我们这里并不涉及，但逻辑是一致的，只是更加复杂。

算术

⭐⭐⭐⭐

所有的算术函数均可直接运用于 array。

⚠️ 需要注意的是：mod 运算可以指定多个被除数。

1
2
3

rng = np.random.default_rng(42)
arr = rng.integers(1, 20, (3, 4))
arr

array([[ 2, 15, 13,  9],
       [ 9, 17,  2, 14],
       [ 4,  2, 11, 19]])

1 2	# +-/ 四则运算，就跟两个数字计算一样 arr 2

array([[ 4, 30, 26, 18],
       [18, 34,  4, 28],
       [ 8,  4, 22, 38]])

1 2	# 平方也可以 arr ** 2

array([[  4, 225, 169,  81],
       [ 81, 289,   4, 196],
       [ 16,   4, 121, 361]])

1 2	# 开方 np.sqrt(arr)

array([[1.41421356, 3.87298335, 3.60555128, 3.        ],
       [3.        , 4.12310563, 1.41421356, 3.74165739],
       [2.        , 1.41421356, 3.31662479, 4.35889894]])

1 2	# log np.log(arr)

array([[0.69314718, 2.7080502 , 2.56494936, 2.19722458],
       [2.19722458, 2.83321334, 0.69314718, 2.63905733],
       [1.38629436, 0.69314718, 2.39789527, 2.94443898]])

1 2	# 超过5的都换成5 np.minimum(arr, 5)

array([[2, 5, 5, 5],
       [5, 5, 2, 5],
       [4, 2, 5, 5]])

1 2	# 低于5的都换成5 np.maximum(arr, 5)

array([[ 5, 15, 13,  9],
       [ 9, 17,  5, 14],
       [ 5,  5, 11, 19]])

1 2	# 四舍五入 np.round(np.sqrt(arr), 2)

array([[1.41, 3.87, 3.61, 3.  ],
       [3.  , 4.12, 1.41, 3.74],
       [2.  , 1.41, 3.32, 4.36]])

1 2	# floor/ceil np.floor(np.sqrt(arr))

array([[1., 3., 3., 3.],
       [3., 4., 1., 3.],
       [2., 1., 3., 4.]])

1	np.ceil(np.sqrt(arr))

array([[2., 4., 4., 3.],
       [3., 5., 2., 4.],
       [2., 2., 4., 5.]])

arr

array([[ 2, 15, 13,  9],
       [ 9, 17,  2, 14],
       [ 4,  2, 11, 19]])

1 2	# mod <=> x % 3 np.mod(arr, 3)

array([[2, 0, 1, 0],
       [0, 2, 2, 2],
       [1, 2, 2, 1]])

arr-5

array([[-3, 10,  8,  4],
       [ 4, 12, -3,  9],
       [-1, -3,  6, 14]])

1 2	# 还可以使用多个被除数 np.mod(arr, arr-5)

array([[-1,  5,  5,  1],
       [ 1,  5, -1,  5],
       [ 0, -1,  5,  5]])

关于广播

numpy 处理不同形状的 array 时使用的手段，极大地方便了使用者。在计算过程中，较小的数组会在较大的数组上进行「广播」，以便适配对方的形状。

⚠️ 需要注意的是：广播需要满足对应的形状。

1
2
3

rng = np.random.default_rng(42)
a = rng.integers(1, 100, (3, 4))
a

array([[ 9, 77, 65, 44],
       [43, 86,  9, 70],
       [20, 10, 53, 97]])

1 2	# 广播，后面的被当做 1 行 4 列 a + [1,2,3,4]

array([[ 10,  79,  68,  48],
       [ 44,  88,  12,  74],
       [ 21,  12,  56, 101]])

1 2	# 或者这样广播，后面的被当做 3 行 1 列 a + [[1], [2], [3]]

array([[ 10,  78,  66,  45],
       [ 45,  88,  11,  72],
       [ 23,  13,  56, 100]])

1 2	# 之前的取余也是可以的 np.mod(a, [1,2,3,4])

array([[0, 1, 2, 0],
       [0, 0, 0, 2],
       [0, 0, 2, 1]])

矩阵

⭐⭐⭐⭐⭐

这一小节主要介绍线性代数中矩阵的处理，我们会介绍几个矩阵相关常用的 API。

⚠️ 需要注意的是：dot 和 matmul 在高维度时表现不同。

rng = np.random.default_rng(42)
a = rng.integers(1, 10, (3, 2))
b = rng.integers(1, 10, (2, 4))
c = rng.integers(1, 10, (3, 3))
a, b, c

(array([[1, 7],
        [6, 4],
        [4, 8]]),
 array([[1, 7, 2, 1],
        [5, 9, 7, 7]]),
 array([[7, 8, 5],
        [2, 8, 5],
        [5, 4, 2]]))

`arr.dot`

1 2	# array 乘法 np.dot(a, b)

array([[ 36,  70,  51,  50],
       [ 26,  78,  40,  34],
       [ 44, 100,  64,  60]])

1 2	# 或者这样乘 a.dot(b)

array([[ 36,  70,  51,  50],
       [ 26,  78,  40,  34],
       [ 44, 100,  64,  60]])

1
2
3

# 我们看下高维度下 dot 和 matmul 的区别
# ijk, lkm -> ijlm
np.dot(np.ones((5, 2, 3)), np.ones((4, 3, 6))).shape

(5, 2, 4, 6)

`np.matmul`

1
2
3

# 矩阵乘法
# 与 dot 的主要区别是：如果维度 > 2，dot 只考虑最后的维度，而 matmul 则考虑所有维度
np.matmul(a, b)

array([[ 36,  70,  51,  50],
       [ 26,  78,  40,  34],
       [ 44, 100,  64,  60]])

1 2	# 同上，写起来比较好看的方法 a @ b

array([[ 36,  70,  51,  50],
       [ 26,  78,  40,  34],
       [ 44, 100,  64,  60]])

1 2	# ijk, ikl -> ijl np.matmul(np.ones((5, 2, 3)), np.ones((4, 3, 6))).shape

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-95-a5c509c4e8f1> in <module>
      1 # ijk, ikl -> ijl
----> 2 np.matmul(np.ones((5, 2, 3)), np.ones((4, 3, 6))).shape


ValueError: operands could not be broadcast together with remapped shapes [original->remapped]: (5,2,3)->(5,newaxis,newaxis) (4,3,6)->(4,newaxis,newaxis) and requested shape (2,6)

1 2	# ijk, ikl -> ijl np.matmul(np.ones((4, 2, 3)), np.ones((4, 3, 6))).shape

(4, 2, 6)

1 2	# 点积 np.vdot(a, a)

1 2	# 对，就是点积 np.sum(a*a)

1 2	# 内积 np.inner(a, a)

array([[50, 34, 60],
       [34, 52, 56],
       [60, 56, 80]])

1 2	# 对，就是内积 a.dot(a.T)

array([[50, 34, 60],
       [34, 52, 56],
       [60, 56, 80]])

1 2	# 行列式 np.linalg.det(c)

-19.999999999999996

1 2	# 逆矩阵（方阵） np.linalg.inv(c)

array([[ 0.2 , -0.2 ,  0.  ],
       [-1.05,  0.55,  1.25],
       [ 1.6 , -0.6 , -2.  ]])

小结和心得

恭喜您学完了 Numpy《从小白到入门》的教程，相信有此基础您在日后足以应付绝大部分的使用场景。如果您还想继续深入学习 Numpy，欢迎关注我们后续课程《从入门到精通》，在那里，我们将深入 numpy 内部细节，对其原理进行系统、全面的介绍。期待我们后会有期。

内容小结

本教程共六个部分，我们给您把最重要的（3个⭐以上的）一些 API 罗列出来供您回忆，加深印象：

创建和生成
- np.linspace(start, end, nums)
- rng.integers/uniform(low, high, size)
- rng.normal(loc, scale, size)
统计和属性
- arr.shape
- arr.sum/max/min(axis, keepdims)
- np.average(arr, axis)
形状和转换
- arr.reshpae/np.reshape
- np.expand_dims(arr, axis)
- np.squeeze(arr axis)
- np.transpose(arr, axis)
- arr.T
分解和组合
- arr[start:stop:step, ...]
- np.concatenate((arr1, arr2), axis)
- np.stack((arr1, arr2), axis)
- np.repeat(arr, repeat_num, axis)
- np.split(arr, part_num, axis)
筛选和过滤
- np.where(condition, arr, replaced_val)
- rng.choice(a, size, replace=False, p=probs_size_equals_a)
- rng.argmax/argmin/argsort(arr, axis)
矩阵和计算
- +-*/
- np.dot(a, b) == a.dot(b)
- np.matmul(a, b) == a @ b

心得技巧

生成/查看 array 时，注意具体的数据类型
很多 API 都有 axis，将它理解为「沿着」或「对」某一维度进行操作就很容易理解了

巩固和练习

接下来，是时候对学到的成果进行一番检验了，为此我们给您准备了两个小菜和一分多餐，请尽情享用。

背景描述：使用 iris 数据集，target 选择 0 和 1（setosa, versicolor），丢弃 2（我们只用二分类就可以了）

基础题目1

切分数据，要求如下：

针对每一 target，分别按 80%/20% 将数据切分为训练数据和测试数据
切分时要求每 5 个样本，取中间的 1 个为测试数据，其余为训练数据

基础题目2

预测结果，要求如下：

加载预先在训练数据上训练好的权重参数（存储参数的方法：np.savez("data/weight", weight=weight)）
使用模型 sigmoid(W·X) 对测试数据进行预测
输出预测的准确率

进阶题目

如果您已经对机器学习有了一定基础，不妨试试这个练习，它会使用更多 numpy 的 API。

使用 Numpy 实现简单神经网络，要求如下：

特征选择第 2 个和第 4 个（sepal width, petal width）
使用反向传播和梯度下降进行学习

提示：

# 数据集
from sklearn.datasets import load_iris

iris = load_iris()
data = iris["data"]
target = iris["target"]

# Sigmoid
def sigmoid(x: np.array, derive: bool = False) -> np.array:
    if derive:
        return x * (1 - x)
    return 1 / (1 + np.exp(-x))

解答和参考

以下是练习题的参考解答。既然是参考，那就一定不是标准，您可以使用任意方式实现最终的目的得到答案。如果您愿意，使用 for 循环也是可以的，但如果最终的答案不对，还是需要重新检查一下。我们特别重视和关注过程，但结果更加重要，条条道路通罗马，咱最后得到罗马不是？

最后再引用《Unix 编程艺术》中的一个观点：先让程序「正确地」运行起来。完成>完美，健康才能快乐。

def sigmoid(x: np.array, derive: bool = False) -> np.array:
    # 求导数（用于反向传播）
    if derive:
        return x * (1 - x)
    return 1 / (1 + np.exp(-x))

from sklearn.datasets import load_iris

# 加载 iris 数据集
iris = load_iris()
# 提取 target ≤ 1 的 target，并将维度从 (length, ) 拓展为 (length, 1)
y = np.expand_dims(np.extract(iris["target"] <= 1, iris["target"]), 1)
# 根据 y 的 size 拿到对应的 x
x = iris["data"][:y.shape[0]]

基础题目1

# 有多少条数据
data_size = x.shape[0]
# 20% 作为测试数据
test_size = int(data_size * 0.2)
# 找到测试数据的 index
test_idx = [2 + i*5 for i in range(test_size)]
# 过滤掉测试数据的 index，剩下的就是训练数据的 index
train_idx = [i for i in range(data_size) if i not in test_idx]

# 使用训练数据的 index 得到训练数据
x_train = x[train_idx]
y_train = y[train_idx]
# 直接使用索引切片得到测试数据，当然也可以使用测试数据 index
x_test = x[2: data_size : 5]
y_test = y[2: data_size : 5]

基础题目2

1
2
3

# 预测函数
def predict(x, w):
    return sigmoid(x.dot(w))

1 2	# 加载权重，注意 key="weight" w = np.load("./data/weight.npz")["weight"]

1 2	# 拿到 sigmoid 的结果，即 probability prob = predict(x_test, w)

1 2	# >（或 ≥）0.5 作为 1 或 0 的标准 sum((prob > 0.5) == y_test) / len(y_test)

array([1.])

进阶题目

1
2
3

# 只取第2和第4个特征
x_train_part = x_train[:, [1, 3]]
x_test_part = x_test[:, [1, 3]]

def test(x, y, wh, wo, use_hidden: bool = False):
    """
    预测函数，如果使用隐层的话，需要增加对应的计算
    """
    if use_hidden:
        ypred = sigmoid(sigmoid(x.dot(wh)).dot(wo))
    else:
        ypred = sigmoid(x.dot(wo))
    print("Acc: %.2f" % (sum((ypred >= 0.5 ) == y) / len(y))[0])

def train(x, y, use_hidden: bool = False, lr: float = 0.01):
    """
    训练函数，可以支持单隐层或无隐层
    """
    hidden_size = 8 if use_hidden else x.shape[1]
    # 初始化，可以有多种初始化方式，我们这里使用 uniform
    wh = np.random.uniform(-np.sqrt(1/hidden_size), np.sqrt(1/hidden_size), (x.shape[1], hidden_size))
    wo = np.random.uniform(-1, 1, (hidden_size, 1))
    # 1000 个 Epoch
    for epoch in range(1, 1001):
        # 使用隐层
        if use_hidden:
            hidden = np.dot(x, wh)
            hidden = sigmoid(hidden)
        else:
            hidden = x
        logits = np.dot(hidden, wo)
        pred = sigmoid(logits)
        
        # 输出层的 error
        pred_err = y - pred
        # 反向传播，输出层的更新权重
        pred_delta = pred_err * sigmoid(pred, True)
        if use_hidden:
            # 隐层的 error 和更新权重
            hidd_err = pred_delta.dot(wo.T)
            hidd_delta = hidd_err * sigmoid(hidden, True)
        
        # 更新参数
        wo += lr * hidden.T.dot(pred_delta)
        if use_hidden:
            wh += lr * x.T.dot(hidd_delta)

        # 计算损失
        loss = np.mean(np.abs(pred_err))
        if epoch % 200 == 0:
            # 如果有验证集，可以在这里对验证集进行验证，结果有提升（如 loss下降或 acc 提高）时进行存储
            # 还可以根据结果提升情况设计自动提前终止的方案（比如连续 3 次不再提升）
            print("Error:" + str(loss))
    
    # 得到训练集的 Acc
    test(x, y, wh, wo, use_hidden)
    # 返回权重（参数）
    return wh, wo

1	wh, wo = train(x_train_part, y_train)

Error:0.12291230663724437
Error:0.08282596392702782
Error:0.06586770282341464
Error:0.056016204876575326
Error:0.049407934168643926
Acc: 1.00

1	test(x_test_part, y_test, wh, wo)

Acc: 1.00

1	wh, wo = train(x_train_part, y_train, True)

Error:0.16416415380726673
Error:0.08236885703184059
Error:0.058163838923958065
Error:0.04626498346103437
Error:0.03903864391270989
Acc: 1.00

1	test(x_test_part, y_test, wh, wo, True)

Acc: 1.00

基本操作

导包

从列表或元组中创建

使用arange生成

使用linespace/logspace生成

数组形状

one/zeros创建

使用random生成

求平均值和标准差

反序和转置

分解和组合

拆分

筛选和过滤

最值索引

矩阵运算

矩阵乘法

原文件

创建和生成

从 python 列表或元组创建

使用 arange 生成

使用 linspace/logspace 生成

np.linspace

使用 ones/zeros 创建

使用 random 生成

从文件读取

统计和属性

尺寸相关

np.shape

最值分位

np.max/min

平均求和标准差

np.average

np.sum

形状和转换

改变形状

np.expand_dims

np.squeeze

np.reshape/arr.reshape

反序

转置

arr.T

np.transpose

分解和组合

切片和索引

index/slice

拼接

np.concatenate

np.stack

重复

分拆

np.split

筛选和过滤

条件筛选

提取

抽样

最值 Index

np.argmax/argmin

np.argsort

矩阵和运算

算术

矩阵

arr.dot

np.matmul

小结和心得

内容小结

心得技巧

巩固和练习

基础题目1

基础题目2

进阶题目

解答和参考

基础题目1

基础题目2

进阶题目

文献和资料

`np.linspace`

`np.shape`

`np.max/min`

`np.average`

`np.sum`

`np.expand_dims`

`np.squeeze`

`np.reshape/arr.reshape`

`arr.T`

`np.transpose`

`index/slice`

`np.concatenate`

`np.stack`

`np.split`

`np.argmax/argmin`

`np.argsort`

`arr.dot`

`np.matmul`